Bernoulli’s Principle is a very important concept in Fluid Mechanics which is the study of fluids (like air and water) and their interaction with other fluids. Bernoulli’s principle is also referred to as Bernoulli’s Equation or Bernoulli Theorem.
This principle was first stated by Daniel Bernoulli and then formulated in Bernoulli’s Equation by Leonhard Euler in 1752, which provides the relationship between the pressure (P) of the fluid flowing, at a height (h) of the container having kinetic and gravitational potential energy.
The conservation of energy was found to be true for flowing fluids by the statement of Bernoulli’s Principle. It may seem contradictory, but Bernoulli’s principle describes how a fluid’s velocity and pressure are related to each other.
In this article, we have provided what is Bernoulli’s principle, Bernoulli’s equation, its derivation, examples, and proof.
What is Bernoulli’s Principle?
Bernoulli’s Principle says that when a fluid is flowing horizontally, the points where the speed is higher exhibit low pressure, while the points where the speed is lower exhibit high pressure. According to Bernoulli’s principle, the gravitational potential energy of elevation, the energy related to fluid pressure, and the kinetic energy of the fluid motion combine up to give the total mechanical energy of a flowing fluid and are all constant.
In real life, Bernoulli’s principle can be observed in rivers. In some places, the width of the river was found to be changed. When the width of the river increases the speed of the water flowing through it decreases. While the speed of water increases in the narrower regions.
Bernoulli’s Principal Definition
Bernoulli’s principle is a fundamental principle in fluid dynamics that relates the pressure within a fluid to the speed of the fluid’s motion
Check: Application of Bernoulli’s Theorem
Bernoulli’s Principle is formulated into an equation called Bernoulli’s Equation. Bernoulli’s Equation is a relationship between kinetic energy, gravitational potential energy, and the pressure of the fluid inside the container.
Thus, Bernoulli’s Principle Formula is stated as:
[Tex]\bold{P+\dfrac{1}{2}\rho v^2+\rho gh=\text{Constant}}
[/Tex]
where,
- P is the Pressure exerted by the fluid,
- ρ is the Density of the fluid,
- v is the Velocity of the fluid,
- g is the Acceleration due to gravity and
- h is the Height of the container.
Bernoulli’s Equation Derivation
Let us consider a container in the shape of a pipe, whose two edges are placed at different heights and varying diameters. The relationship between the areas of cross-sections A, the flow speed v, height from the ground y, and pressure P at two different points 1 and 2 are given in the figure below.
As illustrated in the diagram, the pipe should be at various heights. According to the equation of continuity, its velocity must fluctuate. To achieve this acceleration and force are required, which is produced by the fluid surrounding it, and the pressure in different places must be different.
Before, deriving Bernoulli’s Equation, we assume that the fluid has no viscous forces, so the fluid’s energy will be conserved. Also, the density of the fluid flowing at both points of the container must be uniform.
To determine Bernoulli’s equation, we must first determine how much work done experienced by the fluid,
The work done at point 1 where the force F1 is exerted to displace the fluid to dx1 is
dW1 = F1 dx1
Here, the force exerted at point 1 is given by, F1 = P1A1
where P1 and A1 are the pressure exerted and cross-sectional area at point 1.
This implies,
dW1 = P1A1 dx1
⇒ dW1 = P1 dv
Similarly, the work done by the fluid at point 2 is:
dW2 = P2A2 dx2
⇒ dW2 = P2 dv
Now, the total work done by the fluid flowing through the container is,
dW = P1 dv – P2 dv
⇒ dW = (P1 – P2) dv . . .(1)
Now, the change in the kinetic energy of the fluid is given by,
[Tex]\begin{aligned}\text{d}K&=\dfrac{1}{2}m_2v^2_2-\dfrac{1}{2}m_1v^2_1\end{aligned}
[/Tex]
But, the mass m of the fluid can be written as,
m = ρ dv
Therefore,
[Tex]\begin{aligned}\text{d}K=\dfrac{1}{2}\rho dv (v^2_2-v^2_1)\end{aligned}
[/Tex] . . . (2)
Similarly, the change in gravitational potential energy is given by,
[Tex]\begin{aligned}\text{d}U&=\dfrac{1}{2}m_1gy_2-\dfrac{1}{2}m_2gy_1\\\Rightarrow \text{d}U&=\dfrac{1}{2}\rho dv g(y_2-y_1)\end{aligned}
[/Tex] . . . (3)
According to the law of conservation of energy:
dW = dK + dU
[Tex]\begin{aligned}&(P_1 – P_2) dv=\dfrac{1}{2}\rho dv (v^2_2-v^2_1)+\dfrac{1}{2}\rho dv g(y_2-y_1)\\ \Rightarrow & (P_1-P_2)=\dfrac{1}{2}\rho (v^2_2-v^2_1)+\dfrac{1}{2}\rho g(y_2-y_1)\\ &\Rightarrow P_1+\dfrac{1}{2}\rho v_1^2+\rho gy_1=P_2+\dfrac{1}{2}\rho v_2^2+\rho gy_2\end{aligned}
[/Tex]
This is Bernoulli’s equation and this can be written as a general expression,
[Tex]\bold{P+\frac{1}{2}\rho v^2+\rho gh=\text{Constant} }
[/Tex]
Bernoulli’s Equation at Constant Depth
As the name suggests, let us suppose any fluid is moving at some constant depth, so h1 = h2, under this condition Bernoulli’s equation be
[Tex]P_1+\frac{1}{2}\rho v_1^2+\rho gh_1 = P_2+\frac{1}{2}\rho v_2^2+\rho gh_2
[/Tex]
[Tex]\Rightarrow P_1+\frac{1}{2}\rho v_1^2= P_2+\frac{1}{2}\rho v_2^2
[/Tex] (As h1 = h2 ⇒ ρgh1 = ρgh2)
Bernoulli’s Equation for Static Fluids
Any fluid is said static if there is no motion in it, for example, oil in a container, a calm lake, the air in a room with no air current, etc. For static fluid there is no velocity gradient throughout the fluid, thus v1 = v2. So, under this condition Bernoulli’s equation be.
[Tex]P_1+\frac{1}{2}\rho v_1^2+\rho gh_1 = P_2+\frac{1}{2}\rho v_2^2+\rho gh_2
[/Tex]
[Tex]\Rightarrow P_1+\rho gh_1 = P_2+\rho gh_2
[/Tex]
Now, to simplify it much further, h2 = 0 (any height can be chosen for the reference height to be zero)
[Tex]\Rightarrow P_2 = P_1+\rho gh_1
[/Tex],
This equation tells us that the static pressure increase from point 1 to 2 by ρgh1.
Principle of Continuity
The primary consideration when representing the flow of fluids or gases is continuity. It shows how mass conservation applies to gases and liquids. The law of conservation of mass in fluid dynamics is demonstrated using the continuity equation.
The principle of continuity is stated as, when a incompressible fluid is flowing in a streamline flow then mass passing through the system at different cross-sectional areas are equal.
The flow and behavior of fluids in a pipe are explained by the continuity equation. This formula is used to explain the flow of liquids and gases through pipes, ducts, rivers, etc.
Consider a pipe as shown above, with different cross-sectional areas A1 and A2. Let the rate of mass entering and leaving the given system be M1 and M2 respectively, with a speed of flow v, and density ρ of the fluid.
Then, according to the principle of continuity, the rate of mass of fluid entering must be equal to the rate of mass of fluid leaving the system.
Since, the rate of mass entering, M1 = ρA1V1 Δt and
The rate of mass entering, M2 = ρA2V2 Δt
Therefore,
ρA1V1 Δt = ρA2V2 Δt
ρA1V1= ρA2V2
The above equation is now termed as Equation of Continuity.
Applications of Bernoulli’s Principle and Equation
The following are the important applications of Bernoulli’s Principle:
Venturi Meter
A venturi meter is a device used to measure the rate of flow in a pipe with a non-uniform cross-section.
To the wide and narrow sections of the pipe, we apply Bernoulli’s equation, where h1=h2. The pressure P2 is less than P1 because A1 is bigger than A2, and v2 is greater than v1. The fluid is accelerated as it enters the tube, which is narrow, and slowed as it exits by a net force to the left.
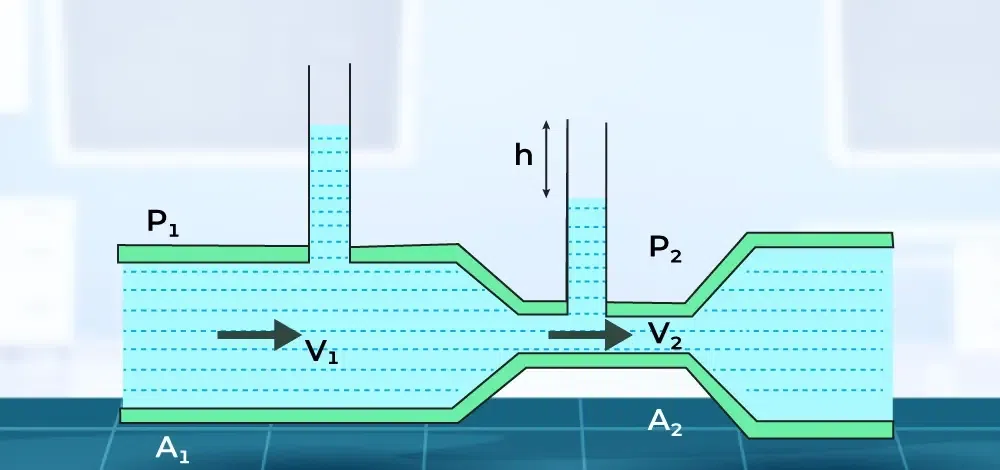
The venturi meter formula is stated as,
[Tex]\bold{v_1=\sqrt{\dfrac{2gh}{\left(\dfrac{A_1}{A_2}\right)^2-1}}}
[/Tex]
where,
- v1 is the rate of fluid flowing,
- g is the acceleration due to gravity,
- h is the difference in liquid level in the two tubes,
- A1 and A2 are the cross-sectional areas of the tube.
Principle of Lifting an Aircraft
Bernoulli’s theorem governs the operation of aeroplanes. The plane’s wings have a certain form. When the plane is moving, the air flows past it at a high rate, despite the plane’s low surface wig.
There is a variation in the flow of air above and below the wings due to Bernoulli’s principle. As a result of the flow of air on the wing’s up surface, this concept causes a change in pressure. If the force is greater than the plane’s mass, the plane will ascend as shown in the figure below:

Action of Atomizer or Spray Gun
When the piston is pulled, air flows out of the horizontal tube, causing the pressure to drop which is less than the container’s pressure. The consequence is that the liquid in the vertical tube rises. When it runs into the fast air in the tube, it dissipates into a thin mist. The same idea governs filter pumps, Bunsen burners, and sprayers used to apply pesticides or scents.

Relation between Conservation of Energy and Bernoulli’s Equation
Bernoulli’s theorem states that the total amount of these three energies within a constantly moving fluid, i.e., kinetic energy, potential energy, and pressure energy, will remain steady throughout the pipeline. However, several factors must be understood:
- The movement of the liquid is assumed to be constant, and there should be no alteration with respect to the pressure, speed, and consistency of the liquid at any point in time. However, if the liquid flow is unstable, there will be a change in speed, and in that case, this equation may not hold true.
- The fluid is considered to be incompressible. Since all liquids are incompressible in nature, this principle can be applied to all fluids. However, in the case of gas flow, there should be a constant density, and one can manage with little difference in pressure, velocity, and temperature.
- Another consideration is the irrotational feature of liquids, which means that the overall angular momentum throughout the liquid is zero.
- The fluid should be ideal for this principle to hold true, meaning there should be no loss of energy due to frictional activity. Hence, there is no excess energy production due to internal particle friction.
Limitations of Bernoulli’s Principle
There are several limitations to Bernoulli’s principle:
- Due to friction, the velocity of fluid particles in the middle of a tube gradually decreases in the tube’s direction. As a result, the liquid’s mean velocity must be used, as the velocity of the particles of the liquid is not constant.
- This Bernoulli equation is effective in streamlining liquid supply, but it is ineffective in turbulent or non-steady flow.
- The liquid flow will be affected by the liquid’s external force.
- This theorem is preferably applied to non-viscous fluids, and an incompressible fluid is required.
- When a fluid is travelling in a curved path, the energy generated by centrifugal forces must be taken into account.
- The liquid flow should remain constant over time.
- A small amount of kinetic energy can be converted to heat energy in an unstable flow, and some energy can be lost due to shear stress in a thick flow. As a result, these losses must be overlooked.
- The effect of viscosity must be negligible.
Also, Read
Solved Examples on Bernoulli’s Principle
Example 1: Water is flowing at a rate of 2m/s through a tube with a diameter of 1 m. If the pressure at this point is 80 kPa, what is the pressure of the water after the tube narrows to a diameter of 0.5m? ρwater=1.0 kgl-1
Solution:
According to Bernoulli’s expression:
[Tex]P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
[/Tex]
The height is same (h1=h2), so the expression can be written as
[Tex]P_{2}=P_{1}+\frac{1}{2}\rho \left(v^2_{1}-v^2_{2}\right)
[/Tex]
The expression for the cross-sectional area is
[Tex]A_{1}=\pi\frac{ d^2}{4}\\ \Rightarrow A_{1}=\pi\frac{ 1^2}{4}\text{ m}^2\\ \Rightarrow A_{1}=\frac{\pi}{4}\text{ m}^2\\
[/Tex]
Similarly
[Tex]A_{2}=\pi\frac{ d^2}{4}\\ \Rightarrow A_{2}=\pi\frac{ 0.5^2}{4}\text{ m}^2\\ \Rightarrow A_{2}=\frac{\pi}{16}\text{ m}^2\\
[/Tex]
The expression for the velocity for each diameter is
[Tex]v_1=\frac{V}{A}\\ \Rightarrow v_1=\frac{2}{\frac{\pi}{4}}\frac{\text{m}}{s}\\ \Rightarrow v_1=\frac{8}{\pi}\frac{\text{m}}{s}
[/Tex]
Similarly,
[Tex]v_2=\frac{2}{\frac{\pi}{16}}\frac{\text{m}}{s}\\ \Rightarrow v_2=\frac{32}{\pi}\frac{\text{m}}{s}
[/Tex]
Substitute the value in Bernoulli’s expression:
[Tex]P_{2}=80000\text{ Pa}+\frac{1}{2}\times1000\frac{\text{kg}}{\text{m}^3}\times\left(\frac{8}{\pi}-\frac{32}{\pi}\right)\frac{\text{m}}{s}\\ \Rightarrow P_{2}=76.2\text{ kPa}
[/Tex]
Example 2: Explain why:
(a) The blood pressure in humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at sea level, though the height of the atmosphere is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though the pressure is force divided by area.
Solution:
(a) The height of the blood column in the foot is greater than that in the brain. As a result, human blood pressure is higher in the feet than in the brain.
(b) The relationship between air density and height is not linear. As a result, pressure does not decrease linearly with height. P = P0e–αh gives the air pressure at a height h, where P0 is the pressure of air at sea level and α is a constant.
(c) When a force is applied to a liquid, the pressure is distributed evenly throughout the liquid. As a result, the pressure due to liquid has no definite direction. As a result, hydrostatic pressure is a scalar value.
Example 3: Drive the expression for Bernoulli’s principle.
Solution:
The flow of an ideal fluid in a pipe of varying cross-section. The fluid in a section of length v1∆t moves to the section of length v2∆t in time ∆t
Consider the flow at two regions BC and DE. Take a look at the flow in two different regions: BC and DE. Consider the fluid that present between B and D would travelled in an infinitesimal time interval ∆t. If v1 is the speed at B and v2 is the speed at D, the fluid at B has travelled a distance of v1∆t to C i.e.
[Tex]dx_{1}=v_{1}\Delta{t}
[/Tex]
In the same interval ∆t the fluid initially at D moves to E, a distance equal to v2∆t i.e.
[Tex]dx_{2}=v_{2}\Delta{t}
[/Tex]
The areas A1 and A2 has the pressures P1 and P2. The work done on the fluid at BC is
[Tex]W_{1}=P_{1}A_{1}\cdot v_{1}\Delta{t}\\ \Rightarrow W_{1}=P_{1}\Delta{V}
[/Tex]
where ∆V is the volume passes through region BC.
Since the same volume ∆V passes through both the regions BC and DE. therefore the expression for the work done by the fluid at the another end DE is
[Tex]W_{2}=P_{2}A_{2}\cdot v_{2}\Delta{t}\\ \Rightarrow W_{2}=P_{2}\Delta{V}
[/Tex]
So the total work done on the fluid is
[Tex]W_{1}-W_{2}=P_{1}\Delta{V}-P_{2}\Delta{V}\\ \Rightarrow W_{1}-W_{2}=\left(P_{1}-P_{2}\right)\Delta{V}
[/Tex]
Let the density of the fluid is ρ therefore the expression ∆m = ρ∆V is the mass passing through the pipe in time ∆t, then change in gravitational potential energy is
[Tex]\Delta{U} =\rho g\Delta{V}\left(h_{2}-h_{1}\right)
[/Tex]
The change in its kinetic energy is given by
[Tex]\Delta{K}=\frac{1}{2}\rho\Delta{V}\left(v^2_{2}-v^2_{1}\right)
[/Tex]
According to he work – energy theorem’
[Tex]\left(P_{1}-P_{2}\right)\Delta{V}=\frac{1}{2}\rho \Delta{V}\left(v^2_{2}-v^2_{1}\right)+\rho g\Delta{V}\left(h_{2}-h_{1}\right)\\ \Rightarrow \left(P_{1}-P_{2}\right)=\frac{1}{2}\rho\left(v^2_{2}-v^2_{1}\right)+\rho g\left(h_{2}-h_{1}\right)
[/Tex]
Rearrange the above expression,
[Tex]P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
[/Tex]
This is Bernoulli’s equation and this can written as general expression.
P + 1/2ρv2 + ρgh = constant
Example 4: Suppose that a huge tank 50m high and filled with water is open to the atmosphere and is hit by a bullet that pierces one side of the tank, allowing water to flow out. The hole is 2m above the ground. If the hole is very small in comparison with the size of the tank, how quickly will the water flow out of the tank?
Solution:
According to Bernoulli’s expression:
[Tex]P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
[/Tex]
According to question it is assumed that the top of the container as point 1, and the hole where water is flowing out as point 2. Both points are open to the atmosphere. Therefore, the pressure on each side of the above equation is equal to 1 atm, and thus it got cancel. The size of the hole on the side of the tank is so small compared to the rest of the tank, the velocity of the water at point 1 is nearly equal to 0. Hence, we can cancel out the 1/2ρ(v1)2 term on the left side of the equation. The expression can rewrite as,
[Tex]\rho gh_1=\frac{1}{2}\rho v^2_{2}+\rho gh_{2}\\ \Rightarrow gh_1=\frac{1}{2}v^2_{2}+gh_{2}\\ \Rightarrow v^2_{2}=2\left(gh_1-gh_2\right)\\ \Rightarrow v_{2}=\sqrt{2g\left(h_1-h_2\right)}\\
[/Tex]
Substitute the values in the above expression,
v2 = √{2×(9.8)×(50-2)}
v2 = 30.67 ms-1
Practice Problems on Bernoulli’s Theorem
Problem 1: A fluid is flowing steadily through a pipe. At one point in the pipe, the fluid has a velocity of 10 m/s and a pressure of 200,000 Pa. If the pipe narrows downstream, and the velocity of the fluid increases to 15 m/s, what is the pressure at that point?
Problem 2: An airplane is flying at a constant altitude. The air pressure on the upper surface of the wing is 90,000 Pa, while the air pressure on the lower surface of the wing is 100,000 Pa. If the speed of the air over the top of the wing is 250 m/s, what is the speed of the air under the wing?
Problem 3: Water is flowing through a hose with a diameter of 2 cm at a speed of 4 m/s. If the hose narrows to a diameter of 1 cm, what is the speed of the water at that point? Assume incompressible flow.
Problem 4: A hydraulic lift is used to lift a car weighing 12,000 N. The piston on which the car sits has an area of 0.2 square meters. If a smaller piston connected to the same hydraulic system has an area of 0.02 square meters, how much force must be applied to the smaller piston to lift the car?
Conclusion of Bernoulli’s Principal
Bernoulli’s principle states that a fluid’s pressure increases with slowing down and decreases with increasing speed. This concept aids in our understanding of many fascinating phenomena, like the functioning of automobile carburetors and water flowing through pipes and airplanes.
Bernoulli’s Principle- FAQs
What is Bernoulli’s Equation?
Bernoulli’s Equation was first explained by Daniel Bernoulli. Bernoulli’s Principle for fluid flow is the basis of Bernoulli’s equation. The total energy of the system is always constant, as shown by Bernoulli’s equation for a fluid. It is stated in accordance with the relationship shown below.
[Tex]\bold{P+\dfrac{1}{2}\rho v^2+\rho gh=\text{Constant}}
[/Tex]
where,
- P is the Pressure exerted by the fluid,
- ρ is the Density of the fluid,
- v is the Velocity of the fluid,
- g is the Acceleration due to gravity and
- h is the Height of the container.
Explain Head Loss in Bernoulli’s Equation.
The drop in total pressure, which is the sum of the velocity head, pressure head, and elevation head of the fluid moving through the hydraulic system, is represented by the head loss in Bernoulli’s equation.
How Chimney Works?
In most cases, the wind speed outside the home is higher than the wind speed inside. Because of the higher wind speed above the chimney’s nozzle, the pressure drops and the air rushes from a high-pressure area to a low-pressure area, which causes the smoke to be blown away by the chimney. Thus, it is simple to see why chimneys perform better when there is a strong wind flow.
Does Bernoulli’s principle apply to water?
Yes, Bernoulli’s principle, which describes the link between changes in pressure and water flow speed, also applies to other fluids.
What are Some Applications of Bernoulli’s Principle?
To solve any incompressible fluid flow problems, use Bernoulli’s equation. Bernoulli’s equation can be used with a venturi meter, nozzle meter, orifice meter, pitot tube, etc. The science of ocean surface waves and acoustics uses Bernoulli’s theory to examine the unstable potential flow.
Bernoulli Equation is based on which Principle?
Bernoulli Equation is based on the Laws of the Conservation of Energy.
What is Bernoulli’s 1st theorem?
According to Bernoulli’s first theorem, as long as the fluid is not subject to any external forces, such as gravity or friction, the total of its kinetic energy (which comes from its motion) potential energy (which comes from its elevation) and pressure energy (which comes from its pressure) remains constant along the path as it flows steadily.
What is the law of Bernoulli?
Bernoulli’s Principle is also called law of Bernoulli.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...