Basic Operations for Queue in Data Structure

Basic Operations on Queue:

Some of the basic operations for Queue in Data Structure are:

• enqueue() – Insertion of elements to the queue.
• dequeue() – Removal of elements from the queue.
• peek() or front()- Acquires the data element available at the front node of the queue without deleting it.
• rear() – This operation returns the element at the rear end without removing it.
• isFull() – Validates if the queue is full.
• isEmpty() – Checks if the queue is empty.
• size(): This operation returns the size of the queue i.e. the total number of elements it contains.  

Queue Data Structure

Operation 1: enqueue()

Inserts an element at the end of the queue i.e. at the rear end.

The following steps should be taken to enqueue (insert) data into a queue:

• Check if the queue is full.
• If the queue is full, return overflow error and exit.
• If the queue is not full, increment the rear pointer to point to the next empty space.
• Add the data element to the queue location, where the rear is pointing.
• return success.

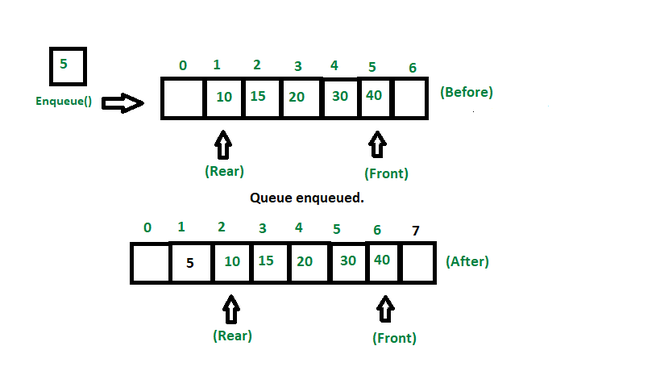
Enqueue representation

Below is the Implementation of the above approach:

C++

void queueEnqueue(int data)
{
    // Check queue is full or not
    if (capacity == rear) {
        printf("\nQueue is full\n");
        return;
    }

    // Insert element at the rear
    else {
        queue[rear] = data;
        rear++;
    }
    return;
}

Java

void queueEnqueue(int data)
{
    // Check queue is full or not
    if (capacity == rear) {
        System.out.println("\nQueue is full\n");
        return;
    }

    // Insert element at the rear
    else {
        queue[rear] = data;
        rear++;
    }
    return;
}

// This code is contributed by aadityapburujwale

C

// Function to add an item to the queue.
// It changes rear and size
void enqueue(struct Queue* queue, int item)
{
    if (isFull(queue))
        return;
    queue->rear = (queue->rear + 1) % queue->capacity;
    queue->array[queue->rear] = item;
    queue->size = queue->size + 1;
    printf("%d enqueued to queue\n", item);
}

// This code is contributed by Susobhan Akhuli

Python3

# Function to add an item to the queue.
# It changes rear and size
def EnQueue(self, item):
    if self.isFull():
        print("Full")
        return
    self.rear = (self.rear + 1) % (self.capacity)
    self.Q[self.rear] = item
    self.size = self.size + 1
    print("% s enqueued to queue" % str(item))
# This code is contributed by Susobhan Akhuli

C#

// Function to add an item to the queue.
// It changes rear and size
public void enqueue(int item)
{
    if (rear == max - 1) {
        Console.WriteLine("Queue Overflow");
        return;
    }
    else {
        ele[++rear] = item;
    }
}

// This code is contributed by Susobhan Akhuli

Javascript

<script>
enqueue(element){
    // adding element to the queue
    this.items.push(element);
}

// This code is contributed by Susobhan Akhuli
</script>

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 2: dequeue()

This operation removes and returns an element that is at the front end of the queue.

The following steps are taken to perform the dequeue operation:

• Check if the queue is empty.
• If the queue is empty, return the underflow error and exit.
• If the queue is not empty, access the data where the front is pointing.
• Increment the front pointer to point to the next available data element.
• The Return success.
  

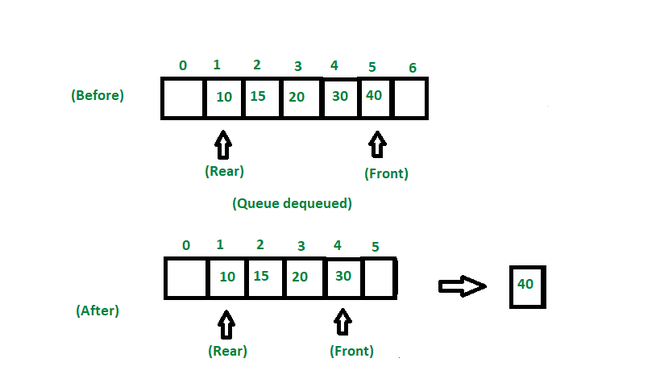
Dequeue operation

Below is the Implementation of above approach:

C++

void queueDequeue()
{
    // If queue is empty
    if (front == rear) {
        printf("\nQueue is empty\n");
        return;
    }

    // Shift all the elements from index 2
    // till rear to the left by one
    else {
        for (int i = 0; i < rear - 1; i++) {
            queue[i] = queue[i + 1];
        }

        // decrement rear
        rear--;
    }
    return;
}

Java

void queueDequeue()
{
    // If queue is empty
    if (front == rear) {
        System.out.println("\nQueue is empty\n");
        return;
    }

    // Shift all the elements from index 2
    // till rear to the left by one
    else {
        for (int i = 0; i < rear - 1; i++) {
            queue[i] = queue[i + 1];
        }

        // decrement rear
        rear--;
    }
    return;
}

// This code is contributed by aadityapburujwale

C

// Function to remove an item from queue.
// It changes front and size
int dequeue(struct Queue* queue)
{
    if (isEmpty(queue)) {
        printf("\nQueue is empty\n");
        return;
    }
    int item = queue->array[queue->front];
    queue->front = (queue->front + 1) % queue->capacity;
    queue->size = queue->size - 1;
    return item;
}

// This code is contributed by Susobhan Akhuli

Python3

# Function to remove an item from queue.
# It changes front and size


def DeQueue(self):
    if self.isEmpty():
        print("Queue is empty")
        return

    print("% s dequeued from queue" % str(self.Q[self.front]))
    self.front = (self.front + 1) % (self.capacity)
    self.size = self.size - 1
# This code is contributed by Susobhan Akhuli

C#

// Function to remove an item from queue.
// It changes front and size
public int dequeue()
{
    if (front == rear + 1) {
        Console.WriteLine("Queue is Empty");
        return -1;
    }
    else {
        int p = ele[front++];
        return p;
    }
}
// This code is contributed by Susobhan Akhuli

Javascript

<script>
dequeue(){
    // removing element from the queue
    // returns underflow when called
    // on empty queue
    if(this.isEmpty()){
        document.write("<br>Queue is empty<br>");
           return -1;
    }
    return this.items.shift();
}
// This code is contributed by Susobhan Akhuli
</script>

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 3: front()

This operation returns the element at the front end without removing it.

The following steps are taken to perform the front operation:

• If the queue is empty return the most minimum value.
• otherwise, return the front value.

Below is the Implementation of the above approach:

C++

// Function to get front of queue
int front(Queue* queue)
{
    if (isempty(queue))
        return INT_MIN;
    return queue->arr[queue->front];
}

Java

// Function to get front of queue
int front(Queue queue)
{
    if (isempty(queue))
        return Integer.MIN_VALUE;
    return queue.arr[queue.front];
}

// This code is contributed by aadityapburujwale

C

// Function to get front of queue
int front(struct Queue* queue)
{
    if (isempty(queue))
        return INT_MIN;
    return queue->arr[queue->front];
}

// This code is contributed by Susobhan Akhuli

Python3

# Function to get front of queue
def que_front(self):
        if self.isempty():
            return "Queue is empty"
        return self.Q[self.front]

# This code is contributed By Susobhan Akhuli

C#

// Function to get front of queue
public int front()
{
    if (isempty())
        return INT_MIN;
    return arr[front];
}

// This code is contributed By Susobhan Akhuli

Javascript

<script>
// Function to get front of queue
front(){
    // returns the Front element of
    // the queue without removing it.
    if(this.isEmpty())
           return "No elements in Queue<br>";
    return this.items[0];
}
// This code is contributed By Susobhan Akhuli
<script>

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 4 : rear()

This operation returns the element at the rear end without removing it.

The following steps are taken to perform the rear operation:

• If the queue is empty return the most minimum value.
• otherwise, return the rear value.

Below is the Implementation of the above approach:

C++

// Function to get rear of queue
int rear(Queue* queue)
{
    if (isEmpty(queue))
        return INT_MIN;
    return queue->arr[queue->rear];
}

Java

// Function to get rear of queue
int rear(Queue queue)
{
    if (isEmpty(queue))
        return Integer.MIN_VALUE;
    return queue.arr[queue.rear];
}

// This code is contributed by aadityapburujwale

C

// Function to get front of queue
int front(struct Queue* queue)
{
    if (isempty(queue))
        return INT_MIN;
    return queue->arr[queue->rear];
}

// This code is contributed by Susobhan Akhuli

Python3

# Function to get rear of queue
def que_rear(self):
        if self.isEmpty():
            return "Queue is empty"
        return self.Q[self.rear]

# This code is contributed By Susobhan Akhuli

C#

// Function to get front of queue
public int front()
{
    if (isempty())
        return INT_MIN;
    return arr[rear];
}

// This code is contributed By Susobhan Akhuli

Javascript

<script>
rear(){
    // returns the Rear element of
    // the queue without removing it.
    if(this.isEmpty())
           return "No elements in Queue<br>";
    return this.items[this.items.length-1];
}
// This code is contributed By Susobhan Akhuli
<script>

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 5: isEmpty():

This operation returns a boolean value that indicates whether the queue is empty or not.

The following steps are taken to perform the Empty operation:

• check if front value is equal to -1 or not, if yes then return true means queue is empty.
• Otherwise return false, means queue is not empty

Below is the implementation of the above approach:

C++

// This function will check whether
// the queue is empty or not:
bool isEmpty()
{
    if (front == -1)
        return true;
    else
        return false;
}

Java

// This function will check whether
// the queue is empty or not:
boolean isEmpty()
{
    if (front == -1)
        return true;
    else
        return false;
}

// This code is contributed by aadityapburujwale

C#

// This function will check whether
// the queue is empty or not:
bool isEmpty()
{
    if (front == -1)
        return true;
    else
        return false;
}

// This code is contributed by lokeshmvs21.

C

// Queue is empty when size is 0
bool isEmpty(struct Queue* queue)
{
    return (queue->size == 0);
}

// This code is contributed by Susobhan Akhuli

Python3

# Queue is empty when size is 0
def isEmpty(self):
    return self.size == 0
# This code is contributed by Susobhan Akhuli

Javascript

</script>
isEmpty(){
    // return true if the queue is empty.
    return this.items.length == 0;
}
// This code is contributed by Susobhan Akhuli
</script>

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 6 : isFull()

This operation returns a boolean value that indicates whether the queue is full or not.

The following steps are taken to perform the isFull() operation:

• Check if front value is equal to zero and rear is equal to the capacity of queue if yes then return true.
• otherwise return false

Below is the Implementation of the above approach:

C++

// This function will check
// whether the queue is full or not.
bool isFull()
{
    if (front == 0 && rear == MAX_SIZE - 1) {
        return true;
    }
    return false;
}

Java

// This function will check
// whether the queue is full or not.
boolean isFull()
{
    if (front == 0 && rear == MAX_SIZE - 1) {
        return true;
    }
    return false;
}

// This code is contributed by aadityapburujwale

C

// Queue is full when size becomes
// equal to the capacity
bool isFull(struct Queue* queue)
{
    return (queue->size == queue->capacity);
}

// This code is contributed by Susobhan Akhuli

C#

// Function to add an item to the queue.
// It changes rear and size
public bool isFull(int item) { return (rear == max - 1); }
// This code is contributed by Susobhan Akhuli

Python3

# Queue is full when size becomes
# equal to the capacity


def isFull(self):
    return self.size == self.capacity

# This code is contributed by Susobhan Akhuli

Javascript

function isFull() {
  if (front == 0 && rear == MAX_SIZE - 1) {
    return true;
  }
  return false;
}

// This code is contributed by aadityamaharshi21.

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)

Operation 7: size()

This operation returns the size of the queue i.e. the total number of elements it contains.

queuename.size()
Parameters :
No parameters are passed
Returns :
Number of elements in the container

C++

// CPP program to illustrate
// Implementation of size() function
#include <iostream>
#include <queue>
using namespace std;

int main()
{
    int sum = 0;
    queue<int> myqueue;
    myqueue.push(1);
    myqueue.push(8);
    myqueue.push(3);
    myqueue.push(6);
    myqueue.push(2);

    // Queue becomes 1, 8, 3, 6, 2

    cout << myqueue.size();

    return 0;
}

Java

// Java program to illustrate implementation of size()
// function

import java.util.*;

public class Main {
    public static void main(String[] args)
    {
        int sum = 0;
        Queue<Integer> myqueue = new LinkedList<>();
        myqueue.add(1);
        myqueue.add(8);
        myqueue.add(3);
        myqueue.add(6);
        myqueue.add(2);

        // Queue becomes 1, 8, 3, 6, 2

        System.out.println(myqueue.size());
    }
}

// This code is contributed by lokesh.

Python

from collections import deque

def main():
    sum = 0
    myqueue = deque()
    myqueue.append(1)
    myqueue.append(8)
    myqueue.append(3)
    myqueue.append(6)
    myqueue.append(2)

    # Queue becomes 1, 8, 3, 6, 2

    print(len(myqueue))

main()

# This code is contributed by aadityamaharshi21.

C#

using System;
using System.Collections.Generic;

namespace ConsoleApp1 {
  class MainClass {
    public static void Main(string[] args)
    {
      int sum = 0;
      Queue<int> myqueue = new Queue<int>();
      myqueue.Enqueue(1);
      myqueue.Enqueue(8);
      myqueue.Enqueue(3);
      myqueue.Enqueue(6);
      myqueue.Enqueue(2);

      // Queue becomes 1, 8, 3, 6, 2

      Console.WriteLine(myqueue.Count);
    }
  }
}

// This code is contributed by adityamaharshi21.

Javascript

// Javascript code
let sum = 0;
let myqueue=[];
myqueue.push(1);
myqueue.push(8);
myqueue.push(3);
myqueue.push(6);
myqueue.push(2);

// Queue becomes 1, 8, 3, 6, 2

console.log(myqueue.length);

Complexity Analysis:
Time Complexity: O(1)
Space Complexity: O(N)