Balanced Prime
Last Updated :
31 Aug, 2022
In number theory, a Balanced Prime is a prime number with equal-sized prime gaps above and below it, so that it is equal to the arithmetic mean of the nearest primes above and below. Or to put it algebraically, given a prime number pn, where n is its index in the ordered set of prime numbers,
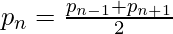
First few balanced prime are 5, 53, 157, 173……
Given a positive integer N. The task is to print Nth balanced prime number.
Examples:
Input : n = 2
Output : 53
Input : n = 3
Output : 157
The idea is to generate prime numbers using Sieve of Eratosthenes and store it in an array. Now iterate over the array to check whether it is balanced prime or not and keep counting the balanced prime. Once you reach the nth prime, return it.
Below is the implementation of this approach:
C++
#include<bits/stdc++.h>
#define MAX 501
using namespace std;
int balancedprime(int n)
{
bool prime[MAX+1];
memset(prime, true, sizeof(prime));
for (int p = 2; p*p <= MAX; p++)
{
if (prime[p] == true)
{
for (int i = p*2; i <= MAX; i += p)
prime[i] = false;
}
}
vector<int> v;
for (int p = 3; p <= MAX; p += 2)
if (prime[p])
v.push_back(p);
int count = 0;
for (int i = 1; i < v.size(); i++)
{
if (v[i] == (v[i+1] + v[i - 1])/2)
count++;
if (count == n)
return v[i];
}
}
int main()
{
int n = 4;
cout << balancedprime(n) << endl;
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static int MAX = 501;
public static int balancedprime(int n)
{
boolean[] prime = new boolean[MAX+1];
for(int k = 0 ; k < MAX+1; k++)
prime[k] = true;
for (int p = 2; p*p <= MAX; p++)
{
if (prime[p] == true)
{
for (int i = p*2; i <= MAX;
i += p)
prime[i] = false;
}
}
Vector<Integer> v =
new Vector<Integer>();
for (int p = 3; p <= MAX; p += 2)
if (prime[p])
v.add(p);
int count = 0;
for (int i = 1; i < v.size(); i++)
{
if ((int)v.get(i) == ((int)v.get(i+1)
+ (int)v.get(i-1))/2)
count++;
if (count == n)
return (int) v.get(i);
}
return 1;
}
public static void main(String[] args)
{
int n = 4;
System.out.print(balancedprime(n));
}
}
|
Python3
MAX = 501
def balancedprime( n ):
prime = [True]*(MAX+1)
p=2
while p * p <= MAX:
if prime[p] == True:
i = p * 2
while i <= MAX:
prime[i] = False
i = i + p
p = p +1
v = list()
p = 3
while p <= MAX:
if prime[p]:
v.append(p)
p = p + 2
count = 0
i=1
for i in range(len(v)):
if v[i] == (v[i+1] + v[i - 1])/2:
count += 1
if count == n:
return v[i]
n = 4
print(balancedprime(n))
|
PHP
<?php
$MAX=501;
function balancedprime($n)
{
global $MAX;
$prime=array_fill(0,$MAX+1,true);
for ($p = 2; $p*$p <= $MAX; $p++)
{
if ($prime[$p] == true)
{
for ($i = $p*2; $i <= $MAX; $i += $p)
$prime[$i] = false;
}
}
$v=array();
for ($p = 3; $p <= $MAX; $p += 2)
if ($prime[$p])
array_push($v,$p);
$count = 0;
for ($i = 1; $i < count($v); $i++)
{
if ($v[$i] == ($v[$i+1] + $v[$i - 1])/2)
$count++;
if ($count == $n)
return $v[$i];
}
}
$n = 4;
echo balancedprime($n);
?>
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
static int MAX = 501;
public static int balancedprime(int n)
{
bool[] prime = new bool[MAX+1];
for(int k = 0 ; k < MAX+1; k++)
prime[k] = true;
for (int p = 2; p*p <= MAX; p++)
{
if (prime[p] == true)
{
for (int i = p*2; i <= MAX;
i += p)
prime[i] = false;
}
}
List<int> v = new List<int>();
for (int p = 3; p <= MAX; p += 2)
if (prime[p])
v.Add(p);
int c = 0;
for (int i = 1; i < v.Count-1; i++)
{
if ((int)v[i]==(int)(v[i+1]+v[i-1])/2)
c++;
if (c == n)
return (int) v[i];
}
return 1;
}
public static void Main()
{
int n = 4;
Console.WriteLine(balancedprime(n));
}
}
|
Javascript
<script>
var MAX = 501;
function balancedprime(n)
{
var prime = Array(MAX+1).fill(true);
for (var p = 2; p*p <= MAX; p++)
{
if (prime[p] == true)
{
for (var i = p*2; i <= MAX; i += p)
prime[i] = false;
}
}
var v = [];
for (var p = 3; p <= MAX; p += 2)
if (prime[p])
v.push(p);
var count = 0;
for (var i = 1; i < v.length; i++)
{
if (v[i] == (v[i+1] + v[i - 1])/2)
count++;
if (count == n)
return v[i];
}
}
var n = 4;
document.write( balancedprime(n) );
</script>
|
Output:
173
Time Complexity: O(m*log(log(m))) where m=MAX(501 in this code)
Auxiliary Space: O(m)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...