Average Velocity
Last Updated :
30 Jun, 2021
It is essential to know how to describe the motion of a body or a particle. These conventions and methods allow us to formalize and then use them to develop further theory. Speed is the notion of how fast a particle is moving. It’s used almost every day and denotes the rate of change of position of an object. In theory, it is essential to describe the speed and the direction of the particle in a formal way. This is done using vectors and this is called velocity. Let’s look at this concept in detail.
Motion in a Plane
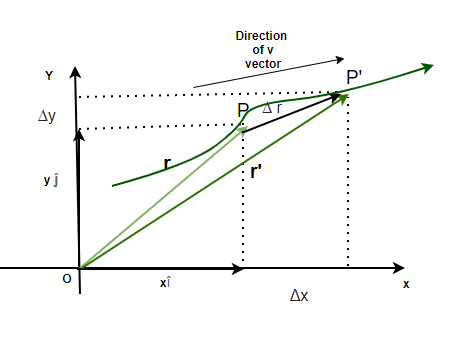
When a particle moves from one point to another point on the X and Y-axis. It is said to be moving on a plane. A plane is made up of X and Y axes, which are used to denote the position of the particle. Motion in a plane is also described in terms of the X and Y coordinates of the particles and how fast they are changing. The motion can be plotted on a Cartesian plane as shown in the figure below.
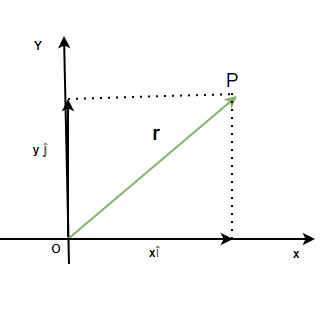
The motion of any particle moving in a plane can be described using its position and its velocity.
Position Vector
The position vector is used to denote the position of the particle on the Cartesian plane with respect to the origin as a reference. The position vector 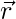 for a particle is given by,
for a particle is given by,
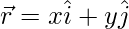
Where x and y are their components along x and y-axis.
Suppose a particle moves from  to
to 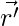 . Then the displacement is directed towards,
. Then the displacement is directed towards,
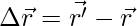
Velocity
The average velocity is the ratio of total displacement over total time. Suppose a particle goes from 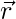 to
to 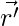 in a total time of
in a total time of 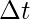
The velocity is given by,
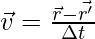
This assumes that the velocity of an object is constant, but this is often not the case. Sometimes, velocity changes with time. In that case, instantaneous velocity should be calculated. It is given by,
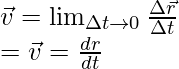
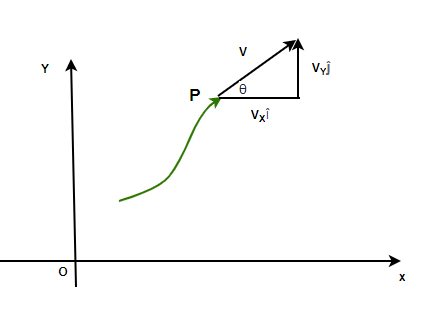
The direction of velocity of a particle following a path at any point is given by a tangent drawn at that particular point in the direction of motion. Velocity can also be expressed in the form of its components.
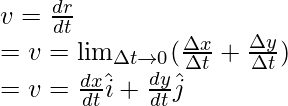
So, if the components of a velocity are known, the magnitude of velocity can be calculated using,
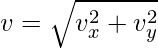
And the direction is given by angle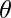 ,
,
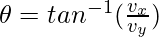
Let’s look at some sample problems.
Sample Problems
Question 1: Find the displacement vector for the particle which is moving in a plane and whose position vectors are given below,
vi = 3i + 4j and vf = 5i + 2j
Answer:
Given: the initial and final position vectors,
vi = 3i + 4j
vf = 5i + 2j
The goal is find the displacement vector. It is given by,
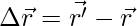
Here 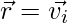 and
and 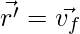
Plugging these values in the equation,
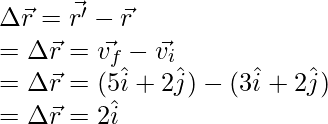
Question 2: Find the displacement vector for the particle which is moving in a plane and whose position vectors are given below,
vi = i + j and vf = 2i + 5j
Answer:
Given: the initial and final position vectors,
vi = i + j
vf = 2i + 5j
The goal is to find the displacement vector. It is given by,
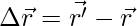
Here 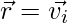 and
and 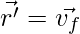
Plugging these values into the equation,
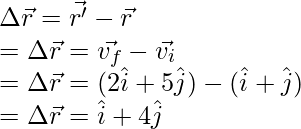
Question 3: Find the velocity at t = 4, for the particle which is moving in a plane and whose position is given below,
r = 2t2i + t3j
Answer:
Given: the initial and final position vectors,
r = 2t2i + t3j
The position vector changes with time. The velocity in this case is given by the formula,
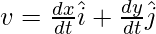
Here x(t) = 2t2 and y(t) = t3
Plugging these values into the equation,
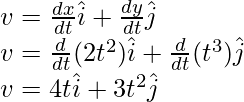
At t = 4,
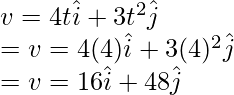
Question 4: Find the velocity at t = 2, for the particle which is moving in a plane and whose position is given below,
r = ti + 4t2j
Answer:
Given: the initial and final position vectors,
r = ti + 4t2j
The position vector changes with time. The velocity in this case is given by the formula,
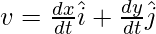
Here x(t) = t and y(t) = 4t2
Plugging these values into the equation,
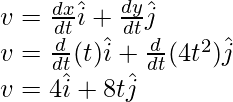
at t = 4,
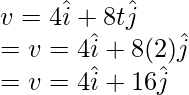
Question 5: Find the average velocity between t = 0 and t = 2, for the particle which is moving in a plane and whose position is given below,
r = 3ti + 3t3j
Answer:
Given: the initial and final position vectors,
r = 3ti + 3t3j
The position vector changes with time. The average velocity is given by the formula,
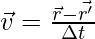
At t = 0
r = 0i + 0j
At t = 2
r’ = 6i + 24j
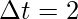
Plugging the values in this above equation,
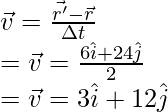
Question 6: Find the average velocity between t = 1 and t = 4, for the particle which is moving in a plane and whose position is given below,
r = ti + tj
Answer:
Given: the initial and final position vectors,
r = ti + tj
The position vector changes with time. The average velocity is given by the formula,
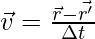
At t = 1
r = 1i + 1j
At t = 4
r’ = 4i + 4j
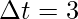
Plugging the values in this above equation,
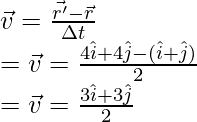
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...