Average of Cubes of first N natural numbers
Last Updated :
14 Mar, 2024
Given a positive integer N, the task is to find the average of cubes of the first N natural numbers.
Examples:
Input: N = 2
Output: 4.5
Explanation:
For integer N = 2,
We have ( 13 + 23 ) = 1 + 8 = 9
average = 9 / 2 that is 4.5
Input: N = 3
Output: 12
Explanation:
For N = 3,
We have ( 13 + 23 + 23 + 23 + 33 + 23 ) = 27 + 8 + 1 = 36
average = 36 / 3 that is 12
Naive Approach: The naive approach is to find the sum of cubes of first N natural numbers and divide it by N.
Below is the implementation of above approach:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find average of cubes
double findAverageOfCube(int n)
{
// Storing sum of cubes
// of numbers in sum
double sum = 0;
// Calculate sum of cubes
for (int i = 1; i <= n; i++) {
sum += i * i * i;
}
// Return average
return sum / n;
}
// Driver Code
int main()
{
// Given Number
int n = 3;
// Function Call
cout << findAverageOfCube(n);
}
// C program for the above approach
#include <stdio.h>
// Function to find average of cubes
double findAverageOfCube(int n)
{
// Store sum of cubes of
// numbers in the sum
double sum = 0;
// Calculate sum of cubes
int i;
for (i = 1; i <= n; i++) {
sum += i * i * i;
}
// Return average
return sum / n;
}
// Driver Code
int main()
{
// Given number
int n = 3;
// Function Call
printf("%lf", findAverageOfCube(n));
return 0;
}
// Java program for the above approach
import java.util.*;
import java.io.*;
class GFG{
// Function to find average of cubes
static double findAverageOfCube(int n)
{
// Storing sum of cubes
// of numbers in sum
double sum = 0;
// Calculate sum of cubes
for (int i = 1; i <= n; i++)
{
sum += i * i * i;
}
// Return average
return sum / n;
}
// Driver Code
public static void main(String[] args)
{
// Given Number
int n = 3;
// Function Call
System.out.print(findAverageOfCube(n));
}
}
// This code is contributed by shivanisinghss2110
// C# program for the above approach
using System;
class GFG{
// Function to find average of cubes
static double findAverageOfCube(int n)
{
// Storing sum of cubes
// of numbers in sum
double sum = 0;
// Calculate sum of cubes
for (int i = 1; i <= n; i++)
{
sum += i * i * i;
}
// Return average
return sum / n;
}
// Driver Code
public static void Main()
{
// Given Number
int n = 3;
// Function Call
Console.Write(findAverageOfCube(n));
}
}
// This code is contributed by Nidhi_biet
<script>
// javascript program for the above approach
// Function to find average of cubes
function findAverageOfCube( n)
{
// Store sum of cubes of
// numbers in the sum
let sum = 0;
// Calculate sum of cubes
let i;
for (i = 1; i <= n; i++) {
sum += i * i * i;
}
// Return average
return sum / n;
}
// Driver Code
// Given number
let n = 3;
// Function Call
document.write(findAverageOfCube(n).toFixed(6));
// This code is contributed by todaysgaurav
</script>
# Python3 program for the above approach
# Function to find average of cubes
def findAverageOfCube(n):
# Storing sum of cubes
# of numbers in sum
sum = 0
# Calculate sum of cubes
for i in range(1, n + 1):
sum += i * i * i
# Return average
return round(sum / n, 6)
# Driver Code
if __name__ == '__main__':
# Given Number
n = 3
# Function Call
print(findAverageOfCube(n))
# This code is contributed by mohit kumar 29
Time complexity: O(N)
Space complexity: O(1)
Efficient Approach:
We know that,
Sum of cubes of first N Natural Numbers =
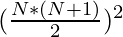
Average is given by:
=>
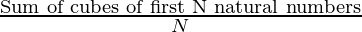
=>
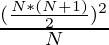
=>
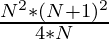
=>
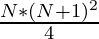
Therefore, the average of the cube sum of first N natural numbers is given by
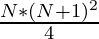
Below is the implementation of above approach:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// function to find an average of cubes
double findAverageofCube(double n)
{
// Apply the formula n(n+1)^2/4
int ans = (n * (n + 1) * (n + 1)) / 4;
return ans;
}
// Driver Code
int main()
{
// Given Number
int n = 3;
// Function Call
cout << findAverageofCube(n);
return 0;
}
// C program for the above approach
#include <stdio.h>
// function to find an average of cubes
double findAverageofCube(double n)
{
// Apply the formula n(n+1)^2/4
int ans = (n * (n + 1) * (n + 1)) / 4;
return ans;
}
// Driver Code
int main()
{
// Given Number
int n = 3;
// Function Call
printf("%f",findAverageofCube(n));
return 0;
}
// Java program for the above approach
class GFG{
// function to find an average of cubes
static double findAverageofCube(double n)
{
// Apply the formula n(n+1)^2/4
int ans = (int)((n * (n + 1) * (n + 1)) / 4);
return ans;
}
// Driver Code
public static void main(String[] args)
{
// Given Number
int n = 3;
// Function Call
System.out.print(findAverageofCube(n));
}
}
// This code is contributed by shivanisinghss2110
// C# program for the above approach
using System;
class GFG{
// function to find an average of cubes
static double findAverageofCube(double n)
{
// Apply the formula n(n+1)^2/4
int ans = (int)((n * (n + 1) * (n + 1)) / 4);
return ans;
}
// Driver Code
public static void Main()
{
// Given Number
int n = 3;
// Function Call
Console.Write(findAverageofCube(n));
}
}
// This code is contributed by Code_Mech
<script>
// javascript program for the above approach
// function to find an average of cubes
function findAverageofCube(n)
{
// Apply the formula n(n+1)^2/4
var ans = parseInt(((n * (n + 1) * (n + 1)) / 4));
return ans;
}
// Driver Code
// Given Number
var n = 3;
// Function Call
document.write(findAverageofCube(n));
// This code is contributed by Amit Katiyar
</script>
# Python3 program for the above approach
# Function to find average of cubes
def findAverageOfCube (n):
# Apply the formula n*(n+1)^2/4
ans = (n * (n + 1) * (n + 1)) / 4
return ans
# Driver code
if __name__ == '__main__':
# Given number
n = 3
# Function call
print(findAverageOfCube(n))
# This code is contributed by himanshu77
Time Complexity: O(1)
Space complexity: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...