Arithmetic Operations of Hexadecimal Numbers
Last Updated :
02 Feb, 2022
Hexadecimal Numbers have a base of 16 digits ranging from 0 to F (i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and A, B, C, D, E, F). A, B, C, D, E, F are equivalent single digits of 10, 11, 12, 13, 14, 15 respectively. Generally, it is expressed by subscript 16 or Hexa (H) or (h).
Arithmetic operations of hexadecimal numbers can be performed using addition table for hexadecimal numbers, which is given as below:
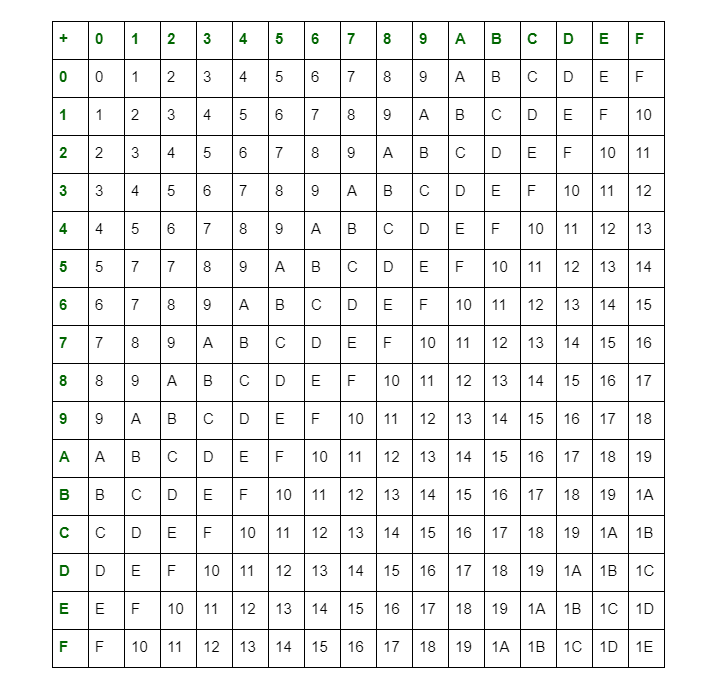
Arithmetic Operations of Hexadecimal Numbers :
- Addition :
We can perform additions of hexadecimal numbers, with the help of the above table
- Subtraction :
Subtraction of hexadecimal numbers can be performed by using complement methods or simply as decimal subtractions. The rule of simple hexadecimal subtraction is the digit borrowed from the immediate higher place is counted as 16.
- Multiplication :
In the multiplication of hexadecimal numbers, if the product is less than radix of hexadecimal (i.e, 16). Then we take it as the result, else divide it by radix of hexadecimal (i.e., 16) and take the remainder as the LSB (the least significant bit). The quotient is taken as carry in the next significant digit. Using these rules, you can make a table for hexadecimal multiplications.
- Division :
Similarly, division of hexadecimal numbers can be performed by following the rules of division of decimal numbers, but the maximum allowed digit will be F(=15 in decimal).
Arithmetic operations of decimal numbers are very popular and much easier. These operations are also performed as the same in other number systems.
Applications of HEX
- In URLs, character codes are written as hexadecimal pairs prefixed with %. As you can see for yourself by googling a symbol @. The link in the address bar of your browser would look like this:
https://www.google.com/search?q=%40
Output:

hexadecimal code
- The HEX numbers are also used for writing programs in low-level languages and in some encoding. For example, in Unicode (a computer standard for symbols encoding), every symbol is represented as a hexadecimal number.
- Also, color schemes are encoded by HEX numbers. In RGB encoding, every color can be represented as 3 hexadecimal numbers, each for Red, Green, or Blue color components respectively.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...