Arithmetic Mean

Arithmetic mean, also called the average or average value, is the quantity obtained by summing two or more numbers or variables and then dividing by the number of numbers or variables. The arithmetic mean is important in statistics. 
For example, Let’s say there are only two quantities involved, the arithmetic mean is obtained simply by adding the quantities and dividing by 2.

Some interesting fact about Arithmetic Mean : 

1. The mean of n numbers x1, x2, . . ., xn is x. If each observation is increased by p, the mean of the new observations is (x + p).
2. The mean of n numbers x1, x2, . . ., xn is x. If each observation is decreased by p, the mean of the new observations is (x – p).
3. The mean of n numbers x1, x2, . . ., xn is x. If each observation is multiplied by a nonzero number p, the mean of the new observations is px.
4. The mean of n numbers x1, x2, . . ., xn is x. If each observation is divided by a nonzero number p, the mean of the new observations is (x/p).

Formula of Arithmetic Mean: 

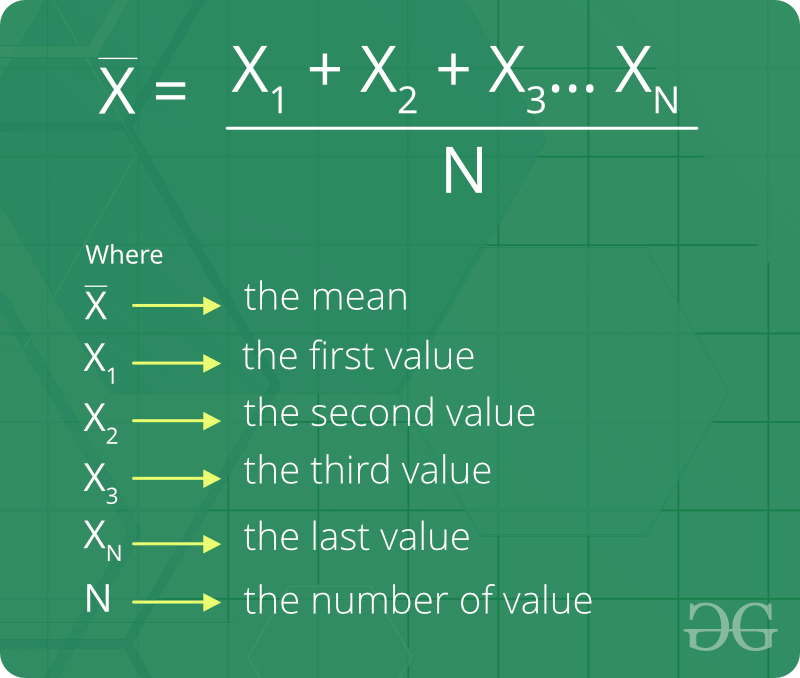
How to find Arithmetic Mean ?
Given three integers A, B and N the task is to find N Arithmetic means between A and B. We basically need to insert N terms in an Arithmetic progression. where A and B are first and last terms.

Examples:

Input : A = 20 B = 32 N = 5
Output : 22 24 26 28 30
The Arithmetic progression series is 
20 22 24 26 28 30 32 

Input : A = 5  B = 35  N = 5
Output : 10 15 20 25 30

Approach :
Let A₁, A₂, A₃, A₄……A_n be N Arithmetic Means between two given numbers A and B . Then A, A₁, A₂ ….. A_n, B will be in Arithmetic Progression. Now B = (N+2)^th term of the Arithmetic progression. So : 

Finding the (N+2)^th term of the Arithmetic progression Series, where d is the Common Difference

B = A + (N + 2 - 1)d
B - A  = (N + 1)d

So the Common Difference d is given by.

d = (B - A) / (N + 1)

We have the value of A and the value of the common difference(d), now we can find all the N Arithmetic Means between A and B. 

C++

// C++ program to find n arithmetic
// means between A and B
#include <bits/stdc++.h>
using namespace std;

// Prints N arithmetic means between
// A and B.
void printAMeans(int A, int B, int N)
{
    // calculate common difference(d)
    float d = (float)(B - A) / (N + 1);

    // for finding N the arithmetic
    // mean between A and B
    for (int i = 1; i <= N; i++)
        cout << (A + i * d) << " ";
}

// Driver code to test above
int main()
{
    int A = 20, B = 32, N = 5;
    printAMeans(A, B, N);
    return 0;
}

Java

// java program to illustrate
// n arithmetic mean between
// A and B
import java.io.*;
import java.lang.*;
import java.util.*;

public class GFG {

    // insert function for calculating the means
    static void printAMeans(int A, int B, int N)
    {
        // Finding the value of d Common difference
        float d = (float)(B - A) / (N + 1);

        // for finding N the Arithmetic
        // mean between A and B
        for (int i = 1; i <= N; i++)
            System.out.print((A + i * d) + " ");
    }

    // Driver code
    public static void main(String args[])
    {
        int A = 20, B = 32, N = 5;
        printAMeans(A, B, N);
    }
}

Python3

# Python3 program to find n arithmetic
# means between A and B

# Prints N arithmetic means
# between A and B.
def printAMeans(A, B, N):

    # Calculate common difference(d)
    d = (B - A) / (N + 1)

    # For finding N the arithmetic
    # mean between A and B
    for i in range(1, N + 1):
        print(int(A + i * d), end = " ")

# Driver code
A = 20; B = 32; N = 5
printAMeans(A, B, N)

# This code is contributed by Smitha Dinesh Semwal

C#

// C# program to illustrate
// n arithmetic mean between
// A and B
using System;

public class GFG {

    // insert function for calculating the means
    static void printAMeans(int A, int B, int N)
    {
        // Finding the value of d Common difference
        float d = (float)(B - A) / (N + 1);

        // for finding N the Arithmetic
        // mean between A and B
        for (int i = 1; i <= N; i++)
            Console.Write((A + i * d) + " ");
    }

    // Driver code
    public static void Main()
    {
        int A = 20, B = 32, N = 5;
        printAMeans(A, B, N);
    }
}
// Contributed by vt_m

PHP

<?php
// PHP program to find n arithmetic
// means between A and B

// Prints N arithmetic means
// between A and B.
function printAMeans($A, $B, $N)
{

    // calculate common
    // difference(d)
    $d = ($B - $A) / ($N + 1);

    // for finding N the arithmetic
    // mean between A and B
    for ($i = 1; $i <= $N; $i++)
        echo ($A + $i * $d), " ";
}

    // Driver Code
    $A = 20; $B = 32;
    $N = 5;
    printAMeans($A, $B, $N);

// This code is Contributed by vt_m.
?>

Javascript

<script>

// Javascript program to find n arithmetic
// means between A and B

// Prints N arithmetic means between
// A and B.
function printAMeans(A, B, N)
{

    // Calculate common difference(d)
    let d = (B - A) / (N + 1);

    // For finding N the arithmetic
    // mean between A and B
    for(let i = 1; i <= N; i++)
        document.write((A + i * d) + " ");
}

// Driver code
let A = 20, B = 32, N = 5;
printAMeans(A, B, N);

// This code is contributed by souravmahato348

</script>

Output:

22 24 26 28 30

Time Complexity: O(N)

Auxiliary Space: O(1)

Basic Program related to Arithmetic Mean 

• Find Harmonic mean using Arithmetic mean and Geometric mean
• Program for class interval arithmetic mean