Area of triangle formed by the axes of co-ordinates and a given straight line

Given a straight line with equation coefficients as a, b & c(ax + by + c = 0), the task is to find the area of the triangle formed by the axes of co-ordinates and this straight line.
Examples:

Input: a = -2, b = 4, c = 3
Output: 0.5625

Input: a = 4, b = 3, c = 12
Output: 6

Approach: 

1. Let PQ be the straight line having AB, the line segment between the axes. 
   The equation is, 
   ax + by + c = 0
   
2. so, in intercept form it can be expressed as, 
   x/(-c/a) + y/(-c/b) = 1
   
3. So, the x-intercept = -c/a
   the y-intercept = -c/b
   
4. So, it is very clear now the base of the triangle AOB will be -c/a
   and the base of the triangle AOB will be -c/b
   
5. So, area of the triangle 
   
   

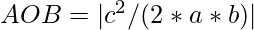
Below is the implementation of the above approach: 

C++

// C++ program area of triangle
// formed by the axes of co-ordinates
// and a given straight line

#include <bits/stdc++.h>
using namespace std;

// Function to find area
double area(double a, double b, double c)
{
    double d = fabs((c * c) / (2 * a * b));
    return d;
}

// Driver code
int main()
{
    double a = -2, b = 4, c = 3;
    cout << area(a, b, c);
    return 0;
}

Java

// Java program area of triangle
// formed by the axes of co-ordinates
// and a given straight line

import java.io.*;

class GFG
{

// Function to find area
static double area(double a, double b, double c)
{
    double d = Math.abs((c * c) / (2 * a * b));
    return d;
}

// Driver code
public static void main (String[] args)
{

    double a = -2, b = 4, c = 3;
    System.out.println(area(a, b, c));
}
}

// This code is contributed by ajit.

Python3

# Python3 program area of triangle
# formed by the axes of co-ordinates
# and a given straight line

# Function to find area
def area(a, b, c):

    d = abs((c * c) / (2 * a * b))
    return d

# Driver code
a = -2
b = 4
c = 3
print(area(a, b, c))

# This code is contributed
# by mohit kumar

C#

// C# program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
using System;

class GFG
{

// Function to find area
static double area(double a, double b, double c)
{
    double d = Math.Abs((c * c) / (2 * a * b));
    return d;
}

// Driver code
static public void Main ()
{

    double a = -2, b = 4, c = 3;
    Console.WriteLine (area(a, b, c));
}
}

// This code is contributed by akt_mit.

PHP

<?php
// PHP program area of triangle
// formed by the axes of co-ordinates
// and a given straight line

// Function to find area
function area($a, $b, $c)
{
    $d = abs(($c * $c) / (2 * $a * $b));
    return $d;
}

// Driver code
$a = -2;
$b = 4;
$c = 3;

echo area($a, $b, $c);

// This code is contributed by Ryuga
?>

Javascript

<script>

// javascript program area of triangle
// formed by the axes of co-ordinates
// and a given straight line

// Function to find area
function area(a , b , c)
{
    var d = Math.abs((c * c) / (2 * a * b));
    return d;
}

// Driver code

var a = -2, b = 4, c = 3;
document.write(area(a, b, c));


// This code is contributed by Amit Katiyar

</script>

Output:

0.5625

Time Complexity: O(1)

Auxiliary Space: O(1)