Area of Equilateral triangle inscribed in a Circle of radius R
Last Updated :
21 Jun, 2022
Given an integer R which denotes the radius of a circle, the task is to find the area of an equilateral triangle inscribed in this circle.
Examples:
Input: R = 4
Output: 20.784
Explanation:
Area of equilateral triangle inscribed in a circle of radius R will be 20.784, whereas side of the triangle will be 6.928
Input: R = 7
Output: 63.651
Explanation:
Area of equilateral triangle inscribed in a circle of radius R will be 63.651, whereas side of the triangle will be 12.124
Approach: Let the above triangle shown be an equilateral triangle denoted as PQR.
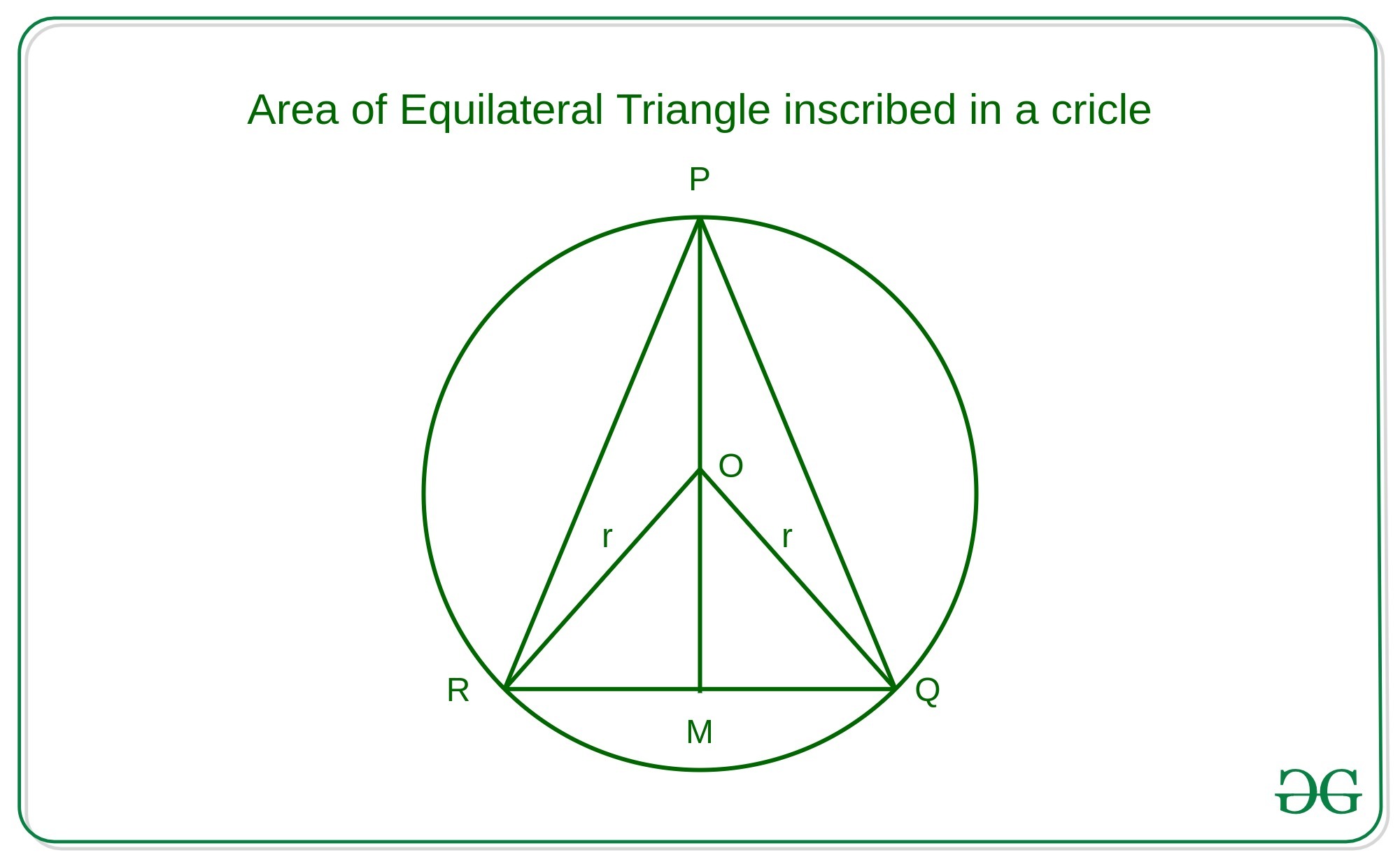
Area of triangle = (1/2) * Base * Height
- In this case, Base can be PQ, PR or QR and The height of the triangle can be PM. Hence,
Area of Triangle = (1/2) * QR * PM
- Now Applying sine law on the triangle ORQ,
RQ OR
------ = -------
sin 60 sin 30
=> RQ = OR * sin60 / sin30
=> Side of Triangle = OR * sqrt(3)
As it is clearly observed
PM = PO + OM = r + r * sin30 = (3/2) * r
- Therefore, the Base and height of the required equilateral triangle will be:
Base = r * sqrt(3) = r * 1.732
Height = (3/2) * r
- Compute the area of the triangle with the help of the formulae given above.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
double area(int R) {
double base = 1.732 * R;
double height = (1.5) * R;
double area = 0.5 * base * height;
return area;
}
int main()
{
int R = 7;
cout<<(area(R));
return 0;
}
|
Java
class GFG
{
static double area(int R) {
double base = 1.732 * R;
double height = (1.5) * R;
double area = 0.5 * base * height;
return area;
}
public static void main(String[] args) {
int R = 7;
System.out.println(area(R));
}
}
|
Python3
def area(R):
base = 1.732 * R
height = ( 3 / 2 ) * R
area = (( 1 / 2 ) * base * height )
return area
if __name__=='__main__':
R = 7
print(area(R))
|
C#
using System;
class GFG
{
static double area(int R)
{
double Base = 1.732 * R;
double height = (1.5) * R;
double area = 0.5 * Base * height;
return area;
}
public static void Main(String[] args)
{
int R = 7;
Console.WriteLine(area(R));
}
}
|
Javascript
<script>
function area(R)
{
var base = 1.732 * R;
var height = (1.5) * R;
var area = 0.5 * base * height;
return area;
}
var R = 7;
document.write(area(R));
</script>
|
Time complexity : O(1)
Auxiliary Space : O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...