Area of Circumcircle of an Equilateral Triangle using Median
Last Updated :
01 Aug, 2022
Given the median of the Equilateral triangle M, the task is to find the area of the circumcircle of this equilateral triangle using the median M.
Examples:
Input: M = 3
Output: 12.5664
Input: M = 6
Output: 50.2655
Approach: The key observation in the problem is that the centroid, circumcenter, orthocenter and incenter of an equilateral triangle all lie at the same point.
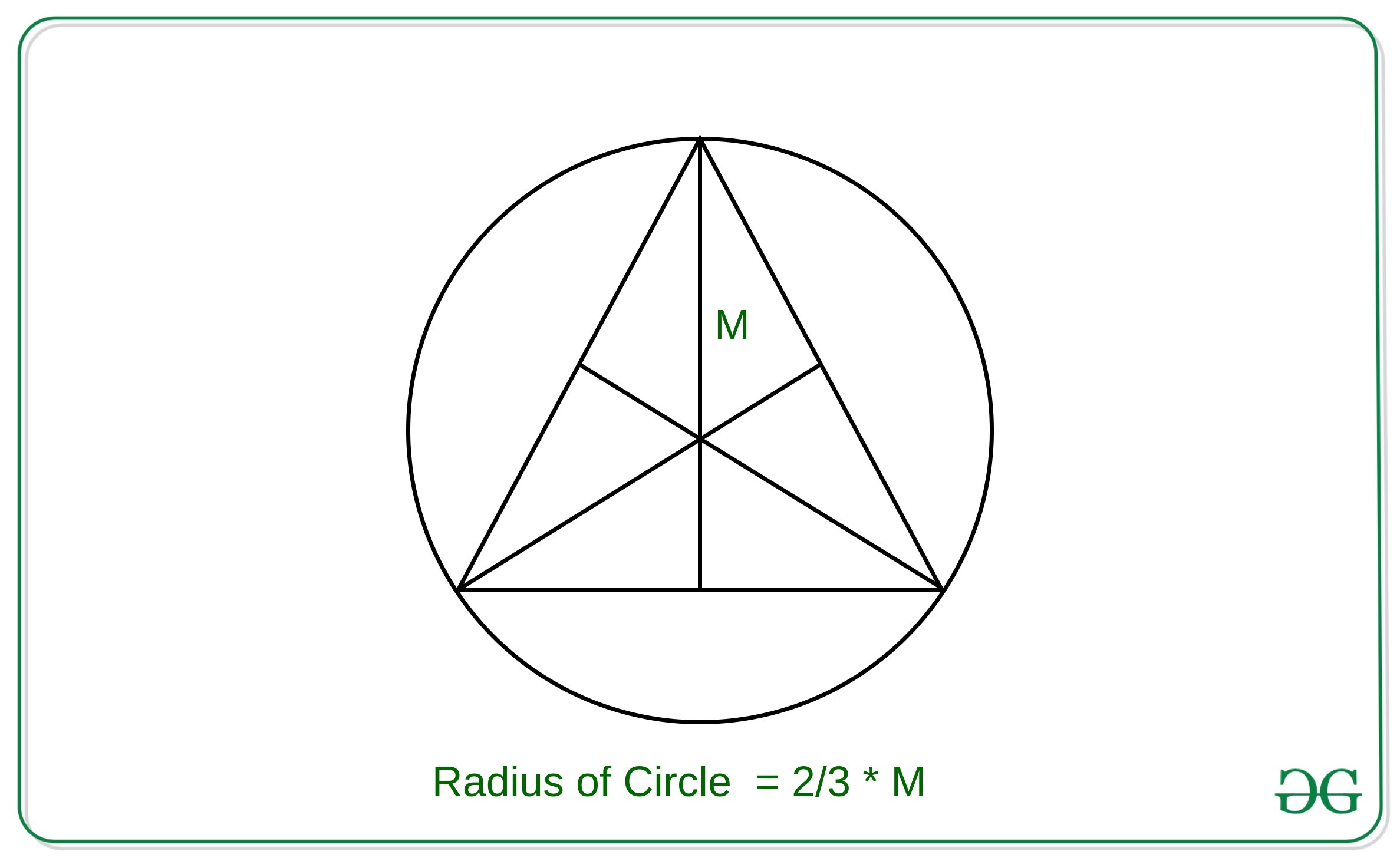
Therefore, the radius of the circle with the given median of the equilateral triangle inscribed in the circle can be derived as:
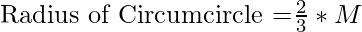
Then the area of the circle can be calculated using the approach used in this article
Below is the implementation of the above approach:
C++
#include <iostream>
const double pi = 3.14159265358979323846;
using namespace std;
void circleArea(double r)
{
cout << (pi * r * r);
}
void findCircleAreaByMedian(double m)
{
double r = 2 * m / 3;
circleArea(r);
}
int main()
{
double m = 3;
findCircleAreaByMedian(m);
return 0;
}
|
Java
import java.util.*;
class GFG{
static double circleArea(double r)
{
double pi = 3.14159265358979323846;
return (pi * r * r);
}
static double findCircleAreaByMedian(int m)
{
double r = 2 * m / 3;
return circleArea(r);
}
public static void main(String args[])
{
int m = 3;
System.out.printf("%.4f", findCircleAreaByMedian(m));
}
}
|
Python3
pi = 3.14159265358979323846
def circleArea(r):
print(round(pi * r * r, 4))
def findCircleAreaByMedian(m):
r = 2 * m /3
circleArea(r)
if __name__ == '__main__':
m = 3
findCircleAreaByMedian(m)
|
C#
using System;
class GFG{
static double circleArea(double r)
{
double pi = 3.14159265358979323846;
return (pi * r * r);
}
static double findCircleAreaByMedian(int m)
{
double r = 2 * m / 3;
return circleArea(r);
}
public static void Main(string []args)
{
int m = 3;
Console.WriteLine("{0:f4}", findCircleAreaByMedian(m));
}
}
|
Javascript
<script>
function circleArea(r) {
var pi = 3.14159265358979323846;
return (pi * r * r);
}
function findCircleAreaByMedian(m) {
var r = 2 * m / 3;
return circleArea(r);
}
var m = 3;
document.write(findCircleAreaByMedian(m).toFixed(4));
</script>
|
Time Complexity: O(1), as we are not using any looping statements.
Auxiliary Space: O(1), as we are not using any extra space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...