Area of Circumcircle of an Equilateral Triangle using Median

Given the median of the Equilateral triangle M, the task is to find the area of the circumcircle of this equilateral triangle using the median M.

Examples:

Input: M = 3 
Output: 12.5664

Input: M = 6 
Output: 50.2655 

Approach: The key observation in the problem is that the centroid, circumcenter, orthocenter and incenter of an equilateral triangle all lie at the same point. 

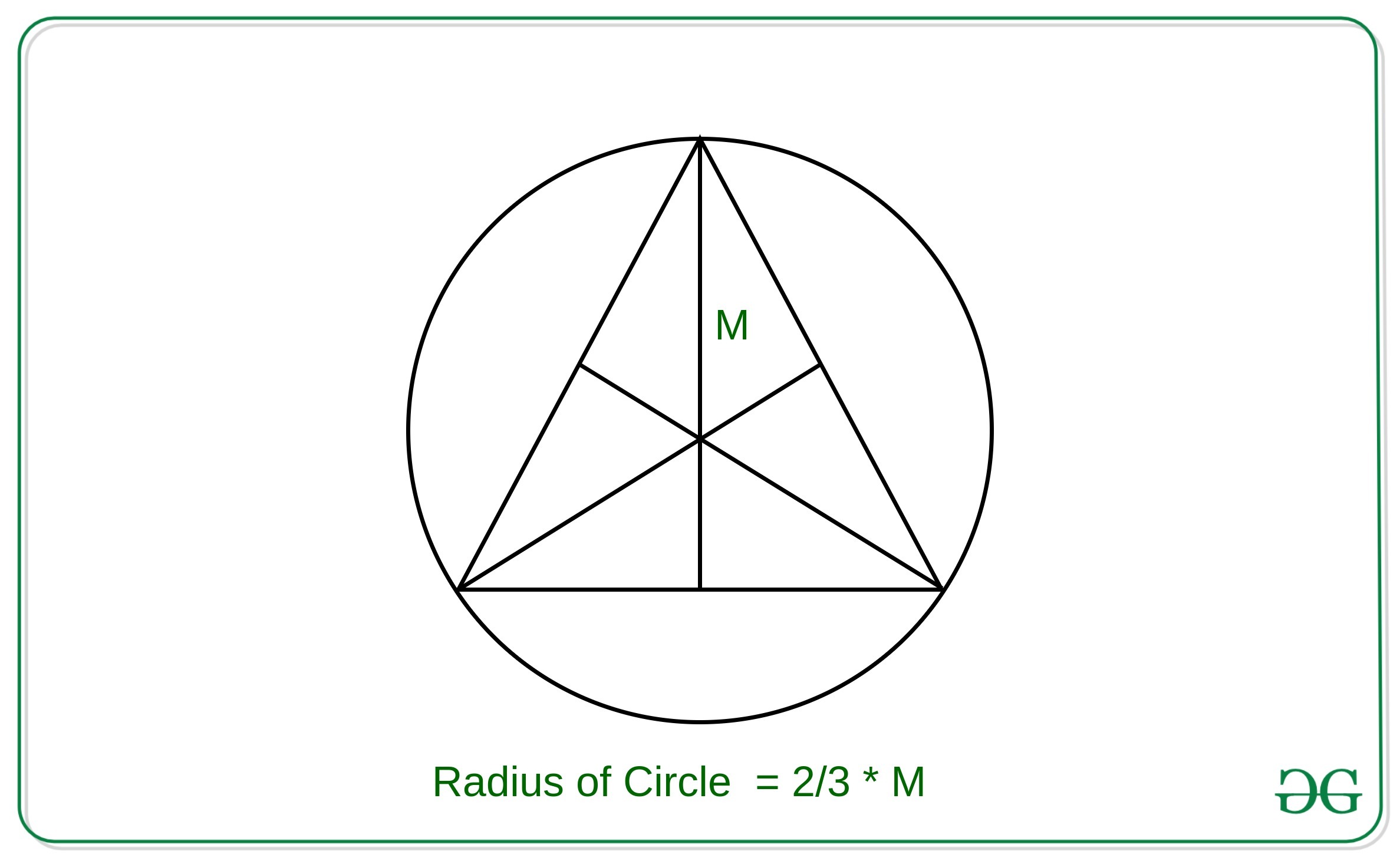
Therefore, the radius of the circle with the given median of the equilateral triangle inscribed in the circle can be derived as: 

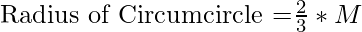
Then the area of the circle can be calculated using the approach used in this article

Below is the implementation of the above approach:

C++

// C++ implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M

#include <iostream>
const double pi = 3.14159265358979323846;
using namespace std;

// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
void circleArea(double r)
{
    cout << (pi * r * r);
}

// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
void findCircleAreaByMedian(double m)
{
    double r = 2 * m / 3;

    // Util Function to find the
    // circle equation
    circleArea(r);
}

// Driver code
int main()
{
    double m = 3;

    // Function Call
    findCircleAreaByMedian(m);
    return 0;
}

Java

// Java implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
import java.util.*;

class GFG{

// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
static double circleArea(double r)
{
    double pi = 3.14159265358979323846;
    return (pi * r * r);
}

// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
static double findCircleAreaByMedian(int m)
{
    double r = 2 * m / 3;

    // Function call to find
    // the circle equation
    return circleArea(r);
}

// Driver code
public static void main(String args[])
{
    int m = 3;

    System.out.printf("%.4f", findCircleAreaByMedian(m));
}
}

// This code is contributed by virusbuddah_

Python3

# Python3 implementation to find the
# equation of circle which inscribes
# equilateral triangle of median M

pi = 3.14159265358979323846

# Function to find the equation
# of circle whose center is (x1, y1)
# and the radius of circle is r
def circleArea(r):

    print(round(pi * r * r, 4))

# Function to find the
# equation of circle which
# inscribes equilateral triangle
# of median M
def findCircleAreaByMedian(m):

    r = 2 * m /3

    # Function to find the
    # circle equation
    circleArea(r)

# Driver code
if __name__ == '__main__':

    m = 3

    # Function call
    findCircleAreaByMedian(m)

# This code is contributed by mohit kumar 29

C#

// C# implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
using System;

class GFG{

// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
static double circleArea(double r)
{
    double pi = 3.14159265358979323846;
    return (pi * r * r);
}

// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
static double findCircleAreaByMedian(int m)
{
    double r = 2 * m / 3;

    // Function call to find
    // the circle equation
    return circleArea(r);
}

// Driver code
public static void Main(string []args)
{
    int m = 3;

    Console.WriteLine("{0:f4}", findCircleAreaByMedian(m));
}
}

// This code is contributed by AnkitRai01

Javascript

<script>
// javascript implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M

    // Function to find the equation
    // of circle whose center is (x1, y1)
    // and the radius of circle is r
    function circleArea(r) {
        var pi = 3.14159265358979323846;
        return (pi * r * r);
    }

    // Function to find the
    // equation of circle which
    // inscribes equilateral triangle
    // of median M
    function findCircleAreaByMedian(m) {
        var r = 2 * m / 3;

        // Function call to find
        // the circle equation
        return circleArea(r);
    }

    // Driver code

    var m = 3;

    document.write(findCircleAreaByMedian(m).toFixed(4));

// This code is contributed by Rajput-Ji
</script>

Output

12.5664

Time Complexity: O(1), as we are not using any looping statements.
Auxiliary Space: O(1), as we are not using any extra space.