Area of circle inscribed in a Isosceles Trapezoid
Last Updated :
21 Jun, 2022
Given two bases of the isosceles trapezoid ABCD as a and b, the task is to find the area of circle inscribed in this trapezoid
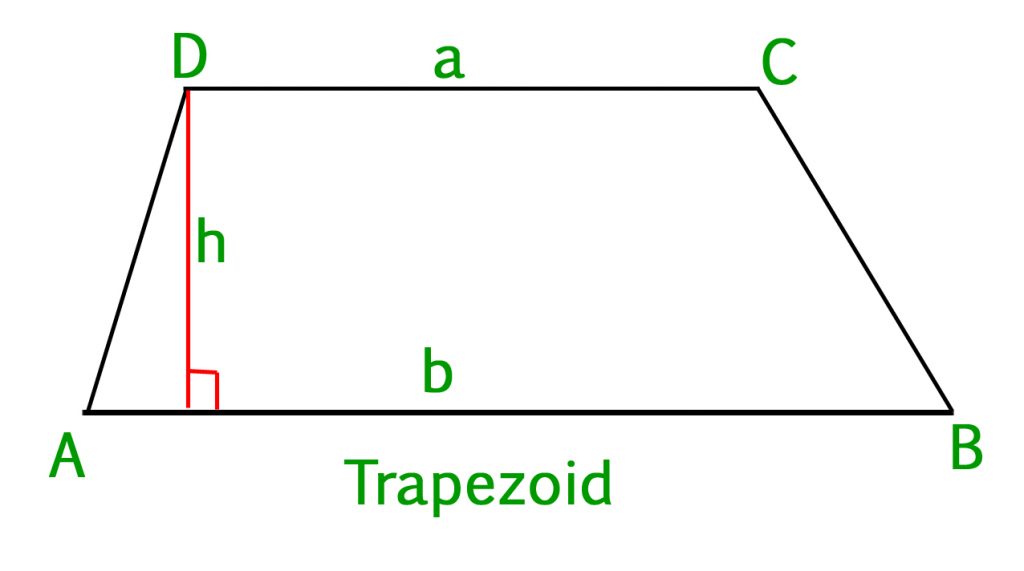
Examples:
Input: a = 10, b = 30
Output: Area = 235.57
Input: a = 20, b = 36
Output: Area = 565.38
Derivation: Given a circle inscribed in trapezium ABCD (sides AB = n and CD = m), we need to find out the height of the trapezium i.e., (AL), which is half of the radius of the circle to find the area of the circle.
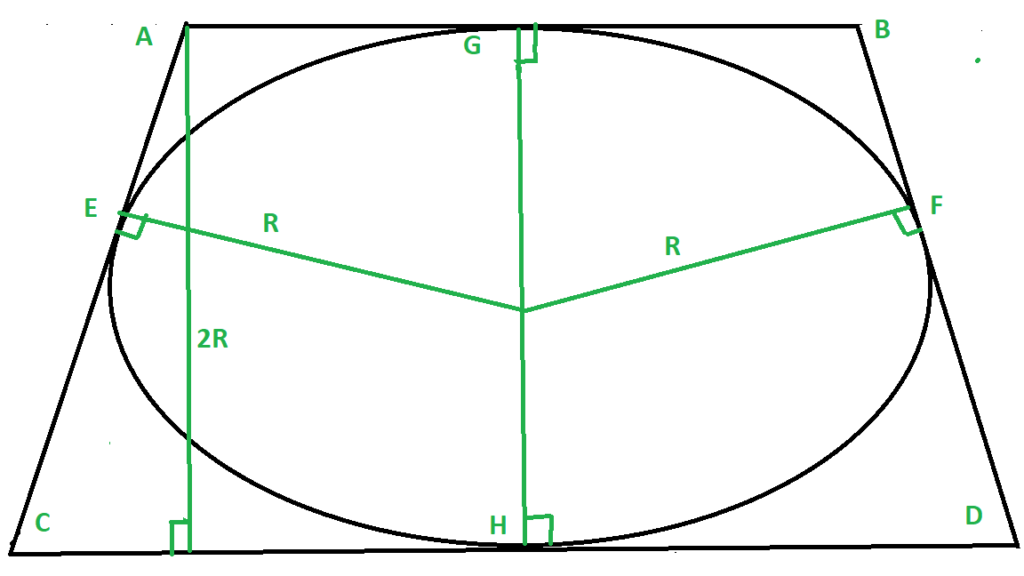
For finding the height of circle we do following operation.
- The circle will always touch the sides of trapezium at their midpoints, Say the midpoints of AB, BD, CD, AC are G, F, H, E, and join them with the center of the circle.
- Now from Symmetry, we can see that
AG = AE = n/2,
EC = CG = m/2,
HD = DF = n/2,
GB = FB = m/2
- Now in Triangle ACL apply the Pythagoras theorem.
Hypotenuse AC = m/2 + n/2
Base CL = CH - AG = m/2 - n/2
we get
Perpendicular AL = Square_root(m * n)
- Therefore the height of the Trapezium = AL = Square_Root(Product of given sides)
- Now the radius of the circle is simple half of the height and hence the area can be calculated easily.
Approach:
- Find the height of the trapezoid as (square_root( m * n )).
- Find the radius of the incircle
R = height / 2
= square_root(m * n) / 2
- Now find the area of the circle
= Pi * R2
= ( 3.141 * m * n ) / 4
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
int main(){
int n = 10;
int m = 30;
cout << (area_of_circle(m, n));
}
|
Java
class GFG
{
static double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
public static void main (String[] args)
{
int n = 10;
int m = 30;
System.out.println(area_of_circle(m, n));
}
}
|
Python3
def area_of_circle(m, n):
square_of_radius = ( m * n ) / 4
area = ( 3.141 * square_of_radius )
return area
if __name__=='__main__':
n = 10
m = 30
print(area_of_circle(m, n))
|
C#
using System;
class GFG
{
static double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
public static void Main ()
{
int n = 10;
int m = 30;
Console.WriteLine(area_of_circle(m, n));
}
}
|
Javascript
<script>
function area_of_circle(m, n)
{
var square_of_radius = ( m * n ) / 4;
var area = ( 3.141 * square_of_radius );
return area;
}
var n = 10;
var m = 30;
document.write(area_of_circle(m, n));
</script>
|
Time complexity: O(1)
space complexity: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...