Area of a Triangle using Determinants is one of the multiple methods available to find the area of a triangle and this method is often overlooked for its complexity. But the Area of a Triangle using Determinants comes very handy in coordinate geometry when all three vertices of a triangle are given and we need to calculate the area of that triangle. In this article, we will cover the methods of calculating area including the Area of a Triangle using Determinants in detail and how to find area using this method as well.
What is Area of a Triangle?
The area occupied by the geometric object triangle is known as the area of a triangle. In other words, the area enclosed by the three sides of a triangle is called the area of a triangle. The area of a triangle is measured in square units as it is the product of two dimensions. There are various formulas for calculating the area of a triangle such as the base height formula, Heron’s Formula, and Formula involving trigonometric ratio sin, and in coordinate geometry when all three vertices are given then we can use determinants as well to calculate the area of a triangle.
Various Formulas for Area of Triangle
If the base of the triangle is denoted by ‘b’ and its height by ‘h’, then the formula for the area of the triangle is:
Area = 1/2 × base × height = 1/2 × b × h
If the lengths of the three sides of the triangle are denoted by ‘a’, ‘b’, and ‘c’, then the area of the triangle can be calculated using Heron’s formula:
Area of Triangle = 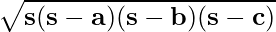
Where s is the semi-perimeter of the triangle i.e., s = (a + b + c)/2
When two sides and the angle between those sides are given then the area of a triangle can be calculated using the following formula:
Area of Triangle = 1/2 × a × b × sin(C)
Where
- ‘a‘ and ‘b‘ are the lengths of two sides of the triangle
- ‘C‘ is the angle between them
Learn more about, Area of a Triangle
What is Area of Triangle in Determinant Form?
The area of a triangle in determinant form is the formula used to find the area of the triangle when the coordinates of the vertices of the triangle are given. This formula uses the concept of the determinant so the name is Area of Triangle in Determinant Form.
Suppose we have to find the area of triangle ABC with vertices A(x1, y1), B(x2, y2), and C(x3, y3), then its area is calculated using the formula,
Area = (1/2) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
This formula is found by solving the determinant that is formed by arranging the coordinates of the vertices of the triangle in the determinant in a specific manner.
Formula for Area of a Triangle using Determinants
The formula for the Area of a Triangle using Determinants is also known as the “shoelace formula” or the “surveyor’s formula.” It is a very straightforward and efficient method of calculating the area of a triangle that can be used to find the area of any shape and sized triangle.
When three vertices of a triangle are given in cartesian coordinates such as (x1, y1), (x2, y2), and (x3, y3), then the area of a triangle is given using the determinant is as follows:
Area of Triangle = 
OR
Area of Triangle =(1/2) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Significance of Abosolute symbol in Formula
As we all know the worth of a determinant can either be a negative or a positive value but since we are talking about an area and it can never be taken as a negative value, therefore we take absolutely the value of the determinant so obtained.
Condition for Collinear Points
Also, if three points are collinear we might be left with a line rather than a triangle and because the area enclosed by a line is zero hence the value of the determinant will also be zero.
How to Find Area of Triangle using Determinant?
To find the area of a triangle using a determinant, we can use the following steps:
Step 1: Let’s say the vertices are A(x1, y1), B(x2, y2), and C(x3, y3).
Step 2: Form a matrix from the coordinates of vertices of triangles as follows.
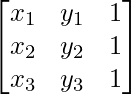
Step 3: Calculate the determinant of the matrix formed in step 2 and take its absolute value.
Step 4: Multiply the result of step 3 by half to get the area of a triangle.
That’s how you can find the area of a triangle using determinants.
Read More,
Area of Triangle in Determinant Form Examples
Example 1: Find the area of the triangle whose vertices are (0, 0), (1, 2), and (4, 3).
Solution:
Let the point (x1, y1) be (0, 0), (x2, y2) be (1, 2) and (x3, y3) be (4, 3).
Area of triangle = 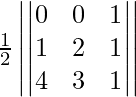
⇒ Area of the triangle= (1/2)|3 – 8|
⇒ Area of the triangle= (1/2)|-5|
⇒ Area of the triangle= 5/2
⇒ Area of the triangle= 2.5
Area cannot be represented with negative. Hence, area of the triangle with given vertices is 2.5 square units.
Example 2: If (k, 2), (2, 4), and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.
Solution:
Given,
Area of triangle = 4 square units
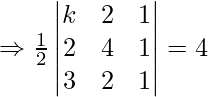
⇒ (1/2){k [4 – 2] – 2[2 – 3] + 1[4 – 12]} = 4
⇒ k(2) – 2(-1) + 1(-8) = 8
⇒ 2k + 2 – 8 = 8
⇒ 2k – 6 = 8
⇒ 2k = 8 + 6
⇒ 2k = 14
⇒ k = 7
So, the value of k is 7.
Example 3: Vertices of a triangle are (-2, -3), (3, 2), and (-1, -8). Find the area of the triangle.
Solution:
Area of the triangle = 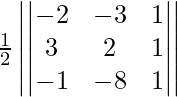
⇒ Area of the triangle = (1/2) |-2(2 + 8) + 3(3+1) + 1(-24 + 2) |
⇒ Area of the triangle = (1/2) |-2 (10) + 3(4) + 1(-22)|
⇒ Area of the triangle = (1/2) | -20 + 12 – 22|
⇒ Area of the triangle = (1/2) |-42 + 12|
⇒ Area of the triangle = (1/2) |-30|
⇒ Area of the triangle = 15
So, the required area is 15 square units.
FAQs on Area of a Triangle using Determinants
Q1: What is Area of Triangle in Determinant Form?
Answer:
The area of a triangle in determinant form is the formula used to find the area of the triangle when the coordinates of the vertices of the triangle are given. Suppose we have to find the area of triangle ABC with vertices A(x1, y1), B(x2, y2), and C(x3, y3), then its area is calculated using the formula,
Area = (1/2) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Q2: What is Formula for finding Area of Triangle using Determinants?
Answer:
The area of triangle using determinants is given as follows,
- Area of Triangle =

- Area of Triangle = (1/2) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of triangle.
Q3: What does the Determinant of a Matrix represent?
Answer:
The determinant of a matrix represents the volume of parallelopiped formed by the vectors using each column of the given matrix.
Q4: What is the significance of the Absolute Value in the formula?
Answer:
As determinants can be positive as well as negative, thus the absolute value in the formula ensures that the area calculated using this formula always remains positive.
Q5: Can this Formula be used for All Types of Triangles?
Answer:
Yes, this formula can be used for all types of triangles wherever there are coordinates of the triangle are given.
Q6: Is using determinants the only way to Find the Area of a Triangle?
Answer:
No, there are various other ways to find the area of triangle such as base height formula, sine rule, Heron’s formula, etc.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...