Area of a polygon with given n ordered vertices
Last Updated :
13 Jul, 2022
Given ordered coordinates of a polygon with n vertices. Find the area of the polygon. Here ordered means that the coordinates are given either in a clockwise manner or anticlockwise from the first vertex to last.
Examples :
Input : X[] = {0, 4, 4, 0}, Y[] = {0, 0, 4, 4};
Output : 16
Input : X[] = {0, 4, 2}, Y[] = {0, 0, 4}
Output : 8
We can compute the area of a polygon using the Shoelace formula.
Area
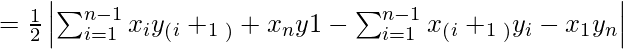
= | 1/2 [ (x1y2 + x2y3 + … + xn-1yn + xny1) –
(x2y1 + x3y2 + … + xnyn-1 + x1yn) ] |
The above formula is derived by following the cross product of the vertices to get the Area of triangles formed in the polygon.
Below is an implementation of the above formula.
CPP
#include <bits/stdc++.h>
using namespace std;
double polygonArea(double X[], double Y[], int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return abs(area / 2.0);
}
int main()
{
double X[] = {0, 2, 4};
double Y[] = {1, 3, 7};
int n = sizeof(X)/sizeof(X[0]);
cout << polygonArea(X, Y, n);
}
|
Java
import java.io.*;
class GFG
{
public static double polygonArea(double X[], double Y[],
int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return Math.abs(area / 2.0);
}
public static void main (String[] args)
{
double X[] = {0, 2, 4};
double Y[] = {1, 3, 7};
int n = 3;
System.out.println(polygonArea(X, Y, n));
}
}
|
Python3
def polygonArea(X, Y, n):
area = 0.0
j = n - 1
for i in range(0,n):
area += (X[j] + X[i]) * (Y[j] - Y[i])
j = i
return int(abs(area / 2.0))
X = [0, 2, 4]
Y = [1, 3, 7]
n = len(X)
print(polygonArea(X, Y, n))
|
C#
using System;
class GFG {
public static double polygonArea(double[] X,
double[] Y, int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++) {
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return Math.Abs(area / 2.0);
}
public static void Main()
{
double[] X = { 0, 2, 4 };
double[] Y = { 1, 3, 7 };
int n = 3;
Console.WriteLine(polygonArea(X, Y, n));
}
}
|
PHP
<?php
function polygonArea($X, $Y, $n)
{
$area = 0.0;
$j = $n - 1;
for ($i = 0; $i < $n; $i++)
{
$area += ($X[$j] + $X[$i]) *
($Y[$j] - $Y[$i]);
$j = $i;
}
return abs($area / 2.0);
}
$X = array(0, 2, 4);
$Y = array(1, 3, 7);
$n = sizeof($X);
echo polygonArea($X, $Y, $n);
?>
|
Javascript
<script>
function polygonArea(X, Y, n)
{
let area = 0.0;
let j = n - 1;
for (let i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return Math.abs(area / 2.0);
}
let X = [0, 2, 4];
let Y = [1, 3, 7];
let n = 3;
document.write(polygonArea(X, Y, n));
</script>
|
Output :
2
Time Complexity: O(n)
Auxiliary Space: O(1), since no extra space has been taken.
Why is it called Shoelace Formula?
The formula is called so because of the way we evaluate it.
Example :
Let the input vertices be
(0, 1), (2, 3), and (4, 7).
Evaluation procedure matches with process of tying
shoelaces.
We write vertices as below
0 1
2 3
4 7
0 1 [written twice]
we evaluate positive terms as below
0 \ 1
2 \ 3
4 \ 7
0 1
i.e., 0*3 + 2*7 + 4*1 = 18
we evaluate negative terms as below
0 1
2 / 3
4 / 7
0 / 1
i.e., 0*7 + 4*3 + 2*1 = 14
Area = 1/2 (18 - 14) = 2
See this for a clearer image.
How does this work?
We can always divide a polygon into triangles. The area formula is derived by taking each edge AB and calculating the (signed) area of triangle ABO with a vertex at the origin O, by taking the cross-product (which gives the area of a parallelogram) and dividing by 2. As one wraps around the polygon, these triangles with positive and negative areas will overlap, and the areas between the origin and the polygon will be canceled out and sum to 0, while only the area inside the reference triangle remains. [Source: Wiki]
For a better understanding look at the following diagrams:
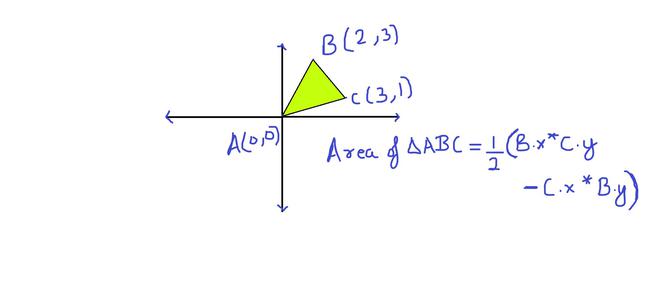
Area Of Triangle Using Cross Product
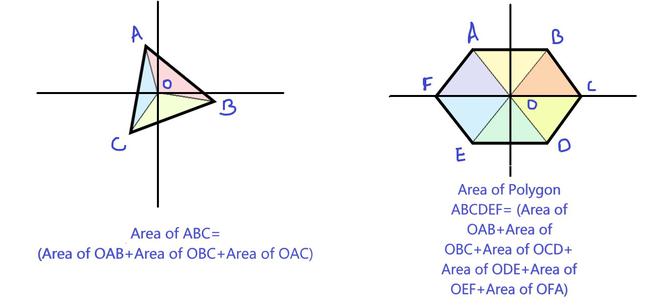
Dividing Polygons into Smaller Triangles to compute Area
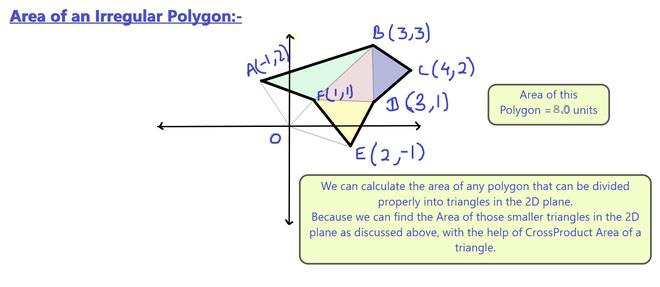
Similarly, for Irregular Polygons, we can form triangles to compute the Area
Related articles :
Minimum Cost Polygon Triangulation
Find Simple Closed Path for a given set of points
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...