Area of a polygon with given n ordered vertices

Given ordered coordinates of a polygon with n vertices. Find the area of the polygon. Here ordered means that the coordinates are given either in a clockwise manner or anticlockwise from the first vertex to last.
Examples :

Input :  X[] = {0, 4, 4, 0}, Y[] = {0, 0, 4, 4};
Output : 16

Input : X[] = {0, 4, 2}, Y[] = {0, 0, 4}
Output : 8

We can compute the area of a polygon using the Shoelace formula.  

Area

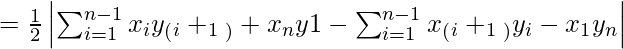
= | 1/2 [ (x₁y₂ + x₂y₃ + … + x_n-1y_n + x_ny₁) –

(x₂y₁ + x₃y₂ + … + x_ny_n-1 + x₁y_n) ] |

The above formula is derived by following the cross product of the vertices to get the Area of triangles formed in the polygon. 
Below is an implementation of the above formula. 

CPP

// C++ program to evaluate area of a polygon using
// shoelace formula
#include <bits/stdc++.h>
using namespace std;

// (X[i], Y[i]) are coordinates of i'th point.
double polygonArea(double X[], double Y[], int n)
{
    // Initialize area
    double area = 0.0;

    // Calculate value of shoelace formula
    int j = n - 1;
    for (int i = 0; i < n; i++)
    {
        area += (X[j] + X[i]) * (Y[j] - Y[i]);
        j = i;  // j is previous vertex to i
    }

    // Return absolute value
    return abs(area / 2.0);
}

// Driver program to test above function
int main()
{
    double X[] = {0, 2, 4};
    double Y[] = {1, 3, 7};

    int n = sizeof(X)/sizeof(X[0]);

    cout << polygonArea(X, Y, n);
}

Java

// Java program to evaluate area
// of a polygon using shoelace formula
import java.io.*;

class GFG
{
    // (X[i], Y[i]) are coordinates of i'th point.
    public static double polygonArea(double X[], double Y[],
                                                       int n)
    {
        // Initialize area
        double area = 0.0;

        // Calculate value of shoelace formula
        int j = n - 1;
        for (int i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);

            // j is previous vertex to i
            j = i;
        }

        // Return absolute value
        return Math.abs(area / 2.0);
    }

    // Driver program
    public static void main (String[] args)
    {
        double X[] = {0, 2, 4};
        double Y[] = {1, 3, 7};

        int n = 3;
        System.out.println(polygonArea(X, Y, n));
    }

}
// This code is contributed by Sunnnysingh

Python3

# python3 program to evaluate
# area of a polygon using
# shoelace formula

# (X[i], Y[i]) are coordinates of i'th point.
def polygonArea(X, Y, n):

    # Initialize area
    area = 0.0

    # Calculate value of shoelace formula
    j = n - 1
    for i in range(0,n):
        area += (X[j] + X[i]) * (Y[j] - Y[i])
        j = i   # j is previous vertex to i


    # Return absolute value
    return int(abs(area / 2.0))

# Driver program to test above function
X = [0, 2, 4]
Y = [1, 3, 7]
n = len(X)
print(polygonArea(X, Y, n))

# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# program to evaluate area
// of a polygon using shoelace formula
using System;

class GFG {

    // (X[i], Y[i]) are coordinates of i'th point.
    public static double polygonArea(double[] X,
                               double[] Y, int n)
    {

        // Initialize area
        double area = 0.0;

        // Calculate value of shoelace formula
        int j = n - 1;

        for (int i = 0; i < n; i++) {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);

            // j is previous vertex to i
            j = i;
        }

        // Return absolute value
        return Math.Abs(area / 2.0);
    }

    // Driver program
    public static void Main()
    {
        double[] X = { 0, 2, 4 };
        double[] Y = { 1, 3, 7 };

        int n = 3;
        Console.WriteLine(polygonArea(X, Y, n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP program to evaluate area of
// a polygon using shoelace formula

// (X[i], Y[i]) are
// coordinates of i'th point.
function polygonArea($X, $Y, $n)
{
    // Initialize area
    $area = 0.0;

    // Calculate value of
    // shoelace formula
    $j = $n - 1;
    for ($i = 0; $i < $n; $i++)
    {
        $area += ($X[$j] + $X[$i]) *
                 ($Y[$j] - $Y[$i]);

        // j is previous vertex to i
        $j = $i;
    }

    // Return absolute value
    return abs($area / 2.0);
}

// Driver Code
$X = array(0, 2, 4);
$Y = array(1, 3, 7);

$n = sizeof($X);

echo polygonArea($X, $Y, $n);

// This code is contributed by ajit
?>

Javascript

<script>

// JavaScript program to evaluate area
// of a polygon using shoelace formula

    // (X[i], Y[i]) are coordinates of i'th point.
    function polygonArea(X, Y, n)
    {
        // Initialize area
        let area = 0.0;

        // Calculate value of shoelace formula
        let j = n - 1;
        for (let i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);

            // j is previous vertex to i
            j = i;
        }

        // Return absolute value
        return Math.abs(area / 2.0);
    }

// Driver Code

        let X = [0, 2, 4];
        let Y = [1, 3, 7];

        let n = 3;
        document.write(polygonArea(X, Y, n));

// This code is contributed by target_2.
</script>

Output :

2

Time Complexity: O(n) 
Auxiliary Space: O(1), since no extra space has been taken.

Why is it called Shoelace Formula?
The formula is called so because of the way we evaluate it. 
Example :

Let the input vertices be
 (0, 1), (2, 3), and (4, 7). 

Evaluation procedure matches with process of tying
shoelaces.

We write vertices as below
  0    1
  2    3
  4    7
  0    1  [written twice]

we evaluate positive terms as below
  0  \  1
  2  \  3
  4  \  7
  0     1  
i.e., 0*3 + 2*7 + 4*1 = 18 

we evaluate negative terms as below
  0     1
  2  /  3
  4  /  7
  0  /  1  
i.e., 0*7 + 4*3 + 2*1 = 14

Area = 1/2 (18 - 14) = 2 

See this for a clearer image.

How does this work?
We can always divide a polygon into triangles. The area formula is derived by taking each edge AB and calculating the (signed) area of triangle ABO with a vertex at the origin O, by taking the cross-product (which gives the area of a parallelogram) and dividing by 2. As one wraps around the polygon, these triangles with positive and negative areas will overlap, and the areas between the origin and the polygon will be canceled out and sum to 0, while only the area inside the reference triangle remains. [Source: Wiki] 

For a better understanding look at the following diagrams:

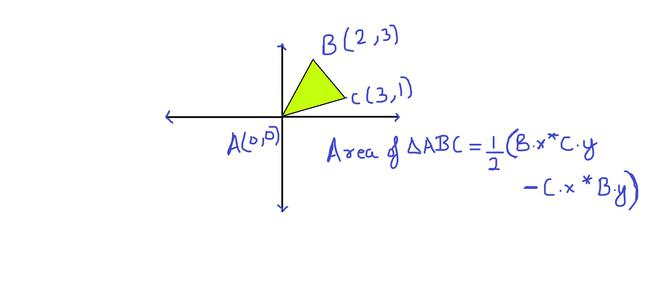
Area Of Triangle Using Cross Product

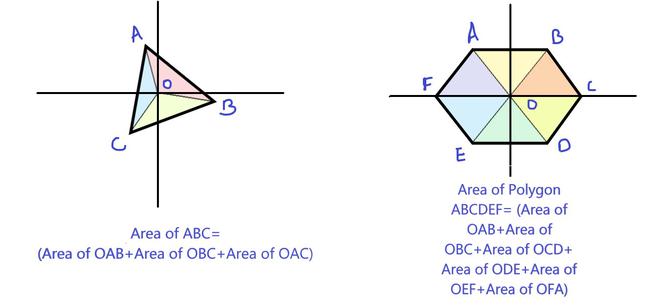
Dividing Polygons into Smaller Triangles to compute Area

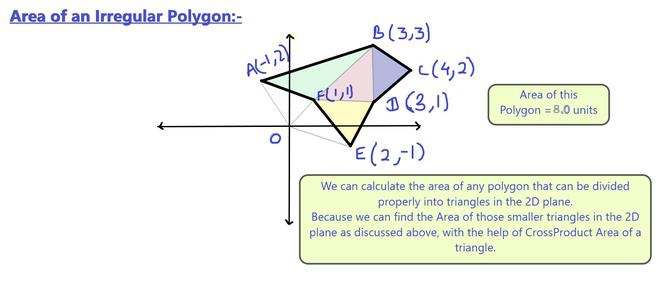
Similarly, for Irregular Polygons, we can form triangles to compute the Area

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above