Area is a quantity that expresses the extent of a two-dimensional figure or shape or planar lamina in the plane. Lamina shapes include 2D figures that can be drawn on a plane, e.g., circle, square, triangle, rectangle, trapezium, rhombus and parallelogram.
A polygon is a two-dimensional shape that is formed by straight lines. The examples of polygons are triangles, hexagons and pentagons.
The names of shapes describe how many sides exist in the shape. For instance, a triangle consists of three sides and a rectangle has four sides. Hence, any shape that can be formed using three straight lines is known as a triangle and any shape that can be drawn by linking four lines is known as a quadrilateral.
The area is the region inside the boundary/perimeter of the shapes which is to be considered.
Area of 2D Shapes
Area of any 2D shape is the size of the region enclosed within it. In geometry, the area can be defined as the space occupied by a flat or the surface of an object. The area of a figure is the number of unit squares that cover the surface of a figure. Area is measured in square units such as square centimetres, square feet, square inches, etc.
SI unit: Square metre (m2)
These are some 2-D Geometries
• Circle
• Rectangle
• Square
• Triangle etc.
Circle
A circle is a closed plane geometric shape. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre. It is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
Basically, a circle is a closed curve with its outer line equidistant from centre. The fixed distance from the point is the radius of the circle.
In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc.
Radius
The radius of the circle is the line which joins the centre of the circle to the outer boundary. It is usually represented by ‘r’ or ‘R’.
In the formula for area and circumference of a circle, radius plays an important role which you will learn later.
Diameter
The diameter of the circle is the line which divides the circle into two equal parts. In an easy way we can say, it is just the double of the radius of the circle and is represented by d’ or ‘D’.
Therefore, d = 2r or D = 2R
If the diameter of the circle is known to us, we can calculate the radius of the circle, such as;
r = d/2 or R = D/2
or
It is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.

Area of circle
Any geometrical shape has its own area. This area is the region that is occupied by the shape in a two-dimensional plane. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle.
Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle’s area.
In geometry, the area enclosed by a circle of radius r is πr². Here, the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 22/7 or 3.14159.
Example: Find Out the area of the following circle.

Given:
Radius of Circle r= 7 cm
Find Out:
Area of Circle=?
Formula Used:
Area of Circle= πr²
Putting the value of r in formula
Area of Circle = 3.14159 × 7 × 7
Area of Circle=154 cm2
Rectangle
Area of rectangle is the region covered by the rectangle in a two-dimensional plane. A rectangle is a 2d shape that has four sides and four vertices. All the four angles of the rectangle are right angles. The opposite sides of the rectangle are equal and parallel to each other.
To be noted, a parallelogram also has its opposite sides equal and parallel to each other but the angles are not equal to 90 degrees. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal; or a parallelogram containing a right angle.
The size of any object can be measured in many ways. For instance, we all normally calculate how tall the building or the size of a swimming pool and how deep it is.
What is the area of a rectangular object, how to find out the area of the rectangle? Lateral and total surface areas can be calculated only for three-dimensional figures. We cannot calculate for the rectangle since it is a two-dimensional figure

Rectangle
Area of Rectangle
Area of rectangle is equal to the multiplication of length and height of the rectangle.
Area of rectangle ABCD = h × l
Example: Find Out the area of the following rectangle

Given:
Length of Rectangle l = 16 cm
Height of Rectangle h = 11 cm
Find Out:
Area of Rectangle =?
Formula Used:
Area of Rectangle = h × l
Putting the value of h and l in formula
Area of Rectangle = 11 × 16
Area of Rectangle =176 cm2
Square
Area of a square is defined as the number of square units needed to fill a square. In general, the area is defined as the region occupied inside the boundary of a flat object or 2d figure. The measurement is done in square units with the standard unit being square meters (m2).
A square is a four-sided polygon (2d Shape), whose four sides are equal in length and all the angles are equal to 90°.
or
A square is a rectangle with all equal sides. The area is the space covered by the object. It is the region occupied by any shape.
While measuring the area of a square, we consider only the length of its side. All the sides of a square are equal and hence, its area is equal to the square of the side.

Square
Area of Square
Area of Square is equal to the square of the side of the Square.
Area of Square = (Side)2
Area of Square = a2
Example: Find Out the area of the following square.

Given:
Side of Rectangle a = 8 cm
Find Out:
Area of Square =?
Formula Used:
Area of Square = a2
Putting the value of h and l in formula
Area of Rectangle = (8cm)2
Area of Rectangle = 64 cm2
Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. In general, the term “area” is defined as the region occupied inside the boundary of a flat object or figure. The measurement is done in square units with the standard unit being square meters (m2).
For the computation of area, there are pre-defined formulas for squares, rectangles, circle, triangles, etc. The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. It is applicable to all types of triangles, whether it is scalene, isosceles, or equilateral. To be noted, the base and height of the triangle are perpendicular to each other.
A triangle with vertices A, B, and C is denoted triangle ABC.
Or
In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane.

Triangle
Area of Triangle
For a given triangle, where the base of the triangle is b and height is h, the area of the triangle can be calculated by the formula, such as;

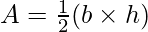
We can also determine the area of the triangle using Heron’s Formula whenever height h is not known. So now we will discuss heron’s formula.
Example: Find out the area of the triangle with height of 13 cm and base of 14 cm.
Given:
Base of Triangle b = 14 cm
Height of Triangle h = 13 cm
Find out: Area of Triangle =?
Formula Used:
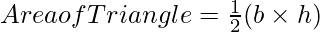
Putting the value of h and l in formula
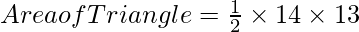
Area of Triangle = 91 cm2
Heron’s Formula
It is also termed as Hero’s Formula. We don’t have to need to know the angle measurement of a triangle to calculate its area. In geometry, Heron’s formula (sometimes called Hero’s formula), named after Hero of Alexandria, gives the area of a triangle when the length of all three sides are known.
Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons.
This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc.
According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle.
Suppose, a triangle ABC, whose sides are a, b and c, respectively. Thus, the area of a triangle can be given by;
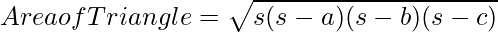
Where
a = length of side a
b = length of side b
c = length of side c
s = semi-perimeter
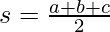
Example: Find Out the area of the following triangle

Given:
First side of Triangle a = 7 cm
Second side of Triangle b = 9 cm
Third side of Triangle c = 10 cm
Find Out:
Area of Triangle =?
Formula Used:
Area of Triangle 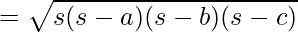
Putting the values in formula
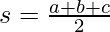
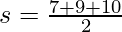
s = 13
Now
Area of Triangle = 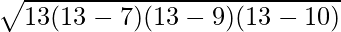
Area of Triangle = 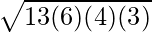
Area of Triangle = 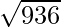
Area of Triangle = 30.59 cm2
Application of Heron’s Formula in finding the area of Quadrilateral
A quadrilateral can be drawn as the sum of two triangles, so we can use Heron’s Formula in finding the area of the quadrilateral. We can understand this using an example
Example: Find out the area of the following quadrilateral using Heron’s Formula.

Given:
Length of quadrilateral l = 12 cm
Height of quadrilateral h = 5 cm
Find Out:
Area of quadrilateral =?
Formula Used:
Area of quadrilateral using Heron’s Formula.
Quadrilateral ABCD can also be draw as sum of two triangles ABD and BCD
We can calculate area of triangles using heron’s Formula where
a = 12 cm
b = 5 cm
c = 13 cm (Using Pythagoras Theorem)
Now area of triangle ABD
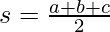
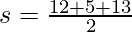
s = 15
Now
Area of Triangle = 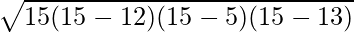
Area of Triangle = 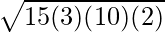
Area of Triangle = 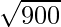
Area of Triangle = 30 cm2
Similarly, area of triangle BCD = 30 cm2
Total Area of ABCD = Area of triangle ABD + Area of triangle BCD
Area of ABCD = 30 cm2 + 30 cm2
Area of ABCD = 60 cm2
We can verify this answer using simple area formula of rectangle which is length × height. Area of rectangle is 12×5 equals to 60 cm2 which is equal using Heron’s Formula.
Example: Find out the area of the triangle with height of 12 cm and base of 9 cm.
Solution:
Given:
Base of Triangle b = 9 cm
Height of Triangle h = 12 cm
Find out: Area of Triangle =?
Formula Used:
Area of Triangle = 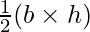
Putting the value of h and l in formula
Area of Triangle = 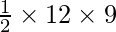
Area of Triangle = 54cm2
Share your thoughts in the comments
Please Login to comment...