Area as Definite Integral
Last Updated :
27 Feb, 2024
Integrals are an integral part of calculus. They represent summation, for the functions which are not as straightforward as the standard functions, integrals help us to calculate the sum and their areas and give us the flexibility to work with any type of functions we want to work with. The areas for the standard functions are already known, it is not easy to keep and remember formulas for the area of every type of function. Integrals provide the generalizability to this and give an approach for calculating these things for any general function. Definite integrals are used to calculate the areas under the curves. Let’s study this concept in detail.
Definite Integrals
Definite integrals are defined as a sum with limits. These are integrals with limits defined as their boundaries between which they calculate the sum for the given function. These limits are called start and end values defined as [a, b] where a is called lower limit and b is called the higher limit of the sum. The definite integral is calculated by calculating the indefinite integral at a and then b and then subtracting both of them.
Given a function f(x) which is continuous between [a, b], this interval is divided into n sub-intervals of width 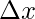 and from each interval a point is chosen x*i. Then the value of the definite integral of the function f(x) from a to b is,
and from each interval a point is chosen x*i. Then the value of the definite integral of the function f(x) from a to b is,
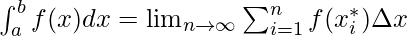
a and b are collectively called interval of integration. This is calculated using the following expression,
Let’s say F(x) = 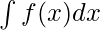

The graph below shows the definite integral of function f(x) working between the interval a and b.

Definite integrals follow sum properties that allow us to simplify our calculations.
Properties of Definite Integrals
Property 1: Limits of any definite integral can be interchanged, a minus sign is added while interchanging the limits.
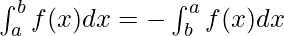
Property 2: If the upper limits and lower limits are equal, then the value of the integral is zero.
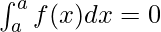
Property 3: When a function is multiplied with a constant, its integral is also multiplied by that constant.

Property 4: Definite integrals can be broken down across sums and differences.
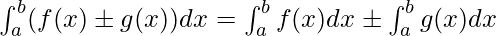
Property 5: The intervals of integrals can be broken down.
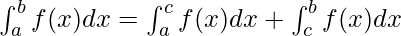
Definite Integrals as Area
Calculation of the area bounded by the curve is one of the most important applications of the integrals. Definite integrals allow us to calculate the area bounded by any curve f(x) between a fixed point x = a and a variable point x.

Now since definite integrals calculate the summation of very small rectangular strips as shown in the above figure, they can be used to calculate the area under the curve. In this case, the area under the curve will be given by,
![Rendered by QuickLaTeX.com \int^{b}_{a}f(x)dx = [F(x)]^{b}_{a} = F(b) - F(a)](https://quicklatex.com/cache3/86/ql_44b2931b7625c9547c2da0a508c42986_l3.png)
Where, F(x) = 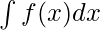
The area bounded by the curve above the x-axis
Consider the function given below in the graph. The function lies completely above the x-axis. We are interested in calculating the area enclosed between this curve and the x-axis between the points x = a and x = b. This case if pretty simple, it just requires us to calculate the area under the curve

So, when the curve lies completely above x-axis the area becomes,

The area bounded by the curve not entirely above the x-axis
In the figure below, some part of the curve lies below the x-axis. The function is f(x) = -x2 + 1

The region of interest is below the x-axis and evaluation of integral in this part leads us to a negative area. This is not possible as the area cannot be negative. If a function lies both above the x-axis and below the x-axis at some points. Then we need to take special care while calculating the area because if they are calculated together, positive and negative areas will cancel each other out, and we will not get the correct value of the area. So, in this case, the limits must be broken down such that both the integrals are separated out, and they should be added with their absolute values.
Let’s say a function is given by f(x), function lies above the x-axis between [0,3] and below the x-axis between (3,∞). The goal is to calculate the area enclosed by the function between [0,5].
So, A = 
⇒A = 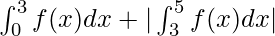
Let’s look at some sample problems
Sample Problems
Question 1: Calculate the area enclosed by the function f(x) and x-axis between x = 0 to x = 1.
f(x) = 3
Answer:
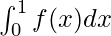
⇒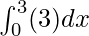
⇒![Rendered by QuickLaTeX.com 3[3x]^{3}_{0}](https://quicklatex.com/cache3/8d/ql_4eec41f2ca3e3136be4437176eb76a8d_l3.png)
⇒![Rendered by QuickLaTeX.com 9[x]^{3}_{0}](https://quicklatex.com/cache3/a0/ql_f9b986bb2bea30bbe1abfa324c7507a0_l3.png)
⇒ 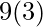
⇒ 27
Question 2: Calculate the area enclosed by the function f(x) and x-axis between x = 0 to x = 3.
f(x) = x2 + 2
Answer:

⇒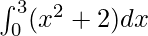
⇒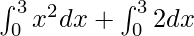
⇒![Rendered by QuickLaTeX.com [\frac{x^3}{3}]^{3}_{0} +[2x]^{3}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bbb1585a0f754609540f14a908a4f43e_l3.png)
⇒![Rendered by QuickLaTeX.com [\frac{3^3}{3} - 0] +[2(3) - 0]](https://quicklatex.com/cache3/51/ql_b2f18449db97a51e3d19abf12ca47151_l3.png)
⇒9 + 6
⇒ 15
Question 3: Calculate the area enclosed by the function f(x) and x-axis between x = 0 to x = 3.
f(x) = 3x
Answer:

⇒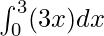
⇒![Rendered by QuickLaTeX.com 3[\frac{x^2}{2}]^{3}_{0}](https://quicklatex.com/cache3/17/ql_8e6ce8d65e7cfdbaf0ae57a87a61b717_l3.png)
⇒![Rendered by QuickLaTeX.com 3[\frac{3^2}{2} - 0]](https://quicklatex.com/cache3/36/ql_06ee3c7b33ab7239cc54810270dac536_l3.png)
⇒ 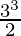
⇒ 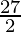
Question 4: Calculate the area enclosed by the function f(x) and x-axis between x = 0 to x = 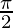 .
.
f(x) = sin(x) + 2
Answer:
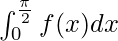
⇒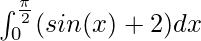
⇒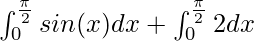
⇒![Rendered by QuickLaTeX.com [-cos(x)]^{\frac{\pi}{2}}_{0} + [2x]^{\frac{\pi}{2}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d7f2a1538126bb6967426dc3b889e2a_l3.png)
⇒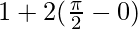
⇒
Question 5: Calculate the area enclosed by the function f(x) and x-axis between x = 0 to x = 1.
f(x) = -ex
Answer:
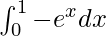
Now this function lies completely below the x-axis, so only the magnitude of the area will be considered, the sign will be ignored.
⇒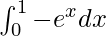
⇒![Rendered by QuickLaTeX.com [-e^x]^{1}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3161a59f5c60132a89377fb72723f1ce_l3.png)
⇒![Rendered by QuickLaTeX.com [e^x]^{0}_{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-67597c755095bcf3eb263056787af5f6_l3.png)
⇒1 – e
Only the magnitude of this area will be considered.
Question 6: Calculate the area by the function f(x) between [0,3].

Solution:
It is obvious from the definition that the function becomes negative after x >=1.
So, the integral must be broken down at x = 1.
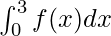
⇒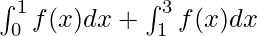
⇒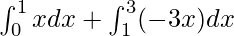
⇒![Rendered by QuickLaTeX.com [\frac{x^2}{2}]^{1}_{0} + [\frac{-3x^2}{2}]^{3}_{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32c3d7e755dc188bb9b521b93ff5437e_l3.png)
⇒![Rendered by QuickLaTeX.com [\frac{1}{2}] + |(-3)[\frac{3^2}{2} - \frac{1^2}{2}]|](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd915a64190b4a7bd8452bc469481e1a_l3.png)
⇒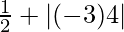
⇒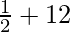
⇒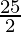
Share your thoughts in the comments
Please Login to comment...