Numbers are the mathematical values or figures used for the purpose of measuring or calculating quantities. It is represented by numerals as 2, 4, 7, etc. Some examples of numbers are integers, whole numbers, natural numbers, rational and irrational numbers, etc.
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals. It is denoted by ‘Q’.
Example: -4, -6, -14, 0, 1, 2, 5, -0.4, 2.10, -2.12, – 5.55 etc.
Rational numbers are of the form p/q, where p and q are integers and q ≠ 0. Because of the underlying structure of numbers, p/q form, most individuals find it difficult to distinguish between fractions and rational numbers.
When a rational number is divided, the output is in decimal form, which can be either ending or repeating. 3, 4, 5, and so on are some examples of rational numbers as they can be expressed in fraction form as 3/1, 4/1, and 5/1 or -0.12 as (-12/100) or (- 2.50) as (-250/100) etc.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Conversion of Decimal number to Rational number
Step 1: Obtain the repeating decimal and put it equal to x.
Step 2: Write the number in decimal form by removing bar from the top of repeating digits and listing repeating digits at least twice. For sample, write x = 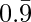 as x = 0.999…. and
as x = 0.999…. and 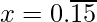 as x = 0.151515……
as x = 0.151515……
Step 3: Determine the number of digits having a bar.
Step 4: If the repeating decimal has 1 place repetition, multiply by 10, if it has a two-place repetition, multiply by 100 and a three-place repetition multiply by 1000 and so on.
Step 5: Subtract the number obtained in Step 2 from the number obtained in Step 4.
Step 6: Divide both sides of the equation by the x coefficient.
Step 7: In the last Write the rational number in its simplest form.
Example: Rewrite the decimal as a rational number. 0.666666666…
Solution: Given: 0.66666.. or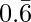
Let’s assume x = 0.66666… ⇢ (1)
And there are one digits after decimal which are repeating, so we will multiply equation 1 both sides by 10.
So 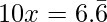 ⇢ (2)
⇢ (2)
Now subtract equation (1) from equation (2)

9x = 6
x = 6/9
= 2/3
0.666666… can be expressed 2/3 as rational number
In this way decimal number can be expressed as a rational number
Are Negative Decimals Rational Numbers?
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals. It is denoted by ‘Q’.
Example: -4, -6, -14, 0, 1, 2, 5, -0.4, 2.10, -2.12, -5.55 etc.
Rational numbers are of the form p/q, where p and q are integers and q ≠ 0. Because of the underlying structure of numbers, p/q form, most individuals find it difficult to distinguish between fractions and rational numbers.
When a rational number is divided, the output is in decimal form, which can be either ending or repeating. 3, 4, 5, and so on are some examples of rational numbers as they can be expressed in fraction form as 3/1, 4/1, and 5/1 or -0.12 as (-12/100) or(- 2.50) as (-250/100) etc.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Here, the answer to above question is YES negative decimals numbers are rational numbers as rational number include all the integers both positive as well as negative integer, decimal as well as fraction because decimal can be written as fraction.
Similar Questions
Question 1: Determine whether -6.1515…. is a rational number.
Answer:
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal. Here, the given number, -6.1515…. has recurring digits.
Hence, -6.1515…. is a rational number.
Question 2: Is negative 0.5 a rational number?
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Here, the given number -0.5 is a rational number as it can be expressed as fraction -0.5 =-5/10
Question 3: Determine whether -7 is a rational number or an irrational number.
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Here, the given number -7 is a rational number.
Question 4: Is -5.56 is a rational number or not?
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
Here, the given number -5.56 is a rational number as integers are the part of rational number.
Question 5: Is -6.56 is a rational number or not?
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
Here, the given number -6.56 is a rational number as integers are the part of rational number.
Question 6: Determine whether -8 is a rational number or an irrational number.
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Here, the given number -8 is a rational number.
Question 7: Is negative 0.7 a rational number?
Answer:
Rational numbers are the numbers that can be expressed as the ratio of two integers. It includes all the integers and can be expressed in terms of fractions or decimals.
A rational number is a sort of real number that has the form p/q where q≠0. When a rational number is split, the result is a decimal number, which can be either a terminating or a recurring decimal.
Here, the given number -0.7 is a rational number as it can be expressed as fraction -0.7 =-7/10
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...