Arden’s Theorem in Theory of Computation
Last Updated :
07 Aug, 2023
Arden’s theorem state that: “If P and Q are two regular expressions over “∑”, and if P does not contain “∈” , then the following equation in R given by R = Q + RP has a unique solution i.e., R = QP*.” That means, whenever we get any equation in the form of R = Q + RP, then we can directly replace it with R = QP*. So, here we will first prove that R = QP* is the solution of this equation and then prove that it is the unique solution of this equation. Let’s start by taking this equation as equation (i)
1. proof R = QP* is the solution of R = Q + RP
R = Q + RP ......(i)
Now, replacing R by R = QP*, we get,
R = Q + QP*P
Taking Q as common,
R = Q( ∈ + P*P) = QP*
(As we know that ∈ + R*R = R*). Hence proved. Thus, R = QP* is the solution of the equation R = Q + RP. Now, we have to prove that this is the only solution to this equation.
2. proof R = QP* is the unique solution of R = Q + RP
Let me take this equation again:
R = Q + RP
Now, replace R by R = Q + RP,
R = Q + (Q + RP)P
= Q + QP + RP2Again, replace R by R = Q + RP :-
R = Q + QP + (Q + RP) P2
= Q + QP + QP2 + RP3
.
.
= Q + QP + QP2 + .. + Q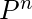 + RP(n+1)
+ RP(n+1)Now, replace R by R = QP*, we get,
R = Q + QP + QP2 + .. + QPn+ QP*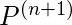
Taking Q as common,
R = Q( ∈ + P + P2 + .. + Pn + P*P(n+1) = QP* [As ∈ + P + P2 + .. + Pn + P*P(n+1)
represent the closure of P]
Hence proved. Thus, R = QP* is the unique solution of the equation R = Q + RP.
Note :
Arden’s theorem is used to convert given finite automata to a regular expression.
To understand this theorem, we will solve an example:
Example –
q1 = q1.0 + ∈
q2 = q1.1 + q2.0
q3 = q2.1 + q3.0 + q3.1
Now,
q1 = ∈ + q1.0q1
= ∈.0* [By Arden's theorem]
q1 = 0* [∈R = R].'.
q2 = 0*1 +q2.0
q2 = 0*10*
[Applying Arden’s theorem]. Hence, the value of q2 is 0*10*.
Features of Arden’s theorem in the context of ToC:
Solving systems of equations: Arden’s theorem provides a method for solving systems of equations involving regular expressions. These systems typically arise in various areas of ToC, such as the construction of finite automata, defining lexical analyzers, or solving pattern matching problems based on regular expressions.
Unique solution: Arden’s theorem guarantees the existence of a unique solution to a given system of equations, assuming the equations satisfy certain conditions. This uniqueness property ensures that the computed solution is unambiguous and reliable.
Efficient and systematic procedure: Arden’s theorem offers a systematic and efficient procedure for finding the solution to a system of equations. It involves iterative substitution and simplification steps, which can be implemented algorithmically. This systematic approach enables the computation of the solution in a structured and organized manner.
Applicability to regular languages: Arden’s theorem is specifically designed for regular languages and regular expressions. Regular languages are fundamental in ToC, and Arden’s theorem provides a powerful tool for solving equations involving regular expressions.
Connection to formal language theory: Arden’s theorem is closely connected to the study of regular languages and formal language theory. It highlights the relationships between regular expressions, regular grammars, and finite automata, which are central concepts in ToC.
Practical implications: The practical implications of Arden’s theorem in ToC are significant. It provides a means for efficiently constructing finite automata from regular expressions, which is crucial in areas such as compiler design, lexical analysis, and text processing. By utilizing Arden’s theorem, engineers and researchers can effectively convert regular expressions into executable and efficient automata-based implementations.
Limitations to regular languages: Arden’s theorem is limited to regular languages and regular expressions. It cannot be directly applied to languages beyond the regular language class, such as context-free or context-sensitive languages. For languages of higher complexity, different techniques and approaches are required.
Share your thoughts in the comments
Please Login to comment...