Apply Formatting in MS Word

Last Updated : 14 Feb, 2023

In MS Word there are multiple types of formatting we can apply to a given text such as Fonts, Font Styles, Font Colors, Font Sizes, Text Highlight Colors, Clearing Formats, Change Cases, etc. Let us apply these techniques to some texts in the Word Processor and see what result it produces.

Font

Fonts are used to change the display of the text or Word Document, look more appealing, and as per the requirement of the situation. There are multiple types of fonts available in MS Word-like: Calibri, Times New Roman, Algerian, Arial, Century, etc.

Steps to Apply:

Step 1: Select the text you want to change the font of.

Step 2: Now, select the font of your choice from the Home menu bar in MS Word.

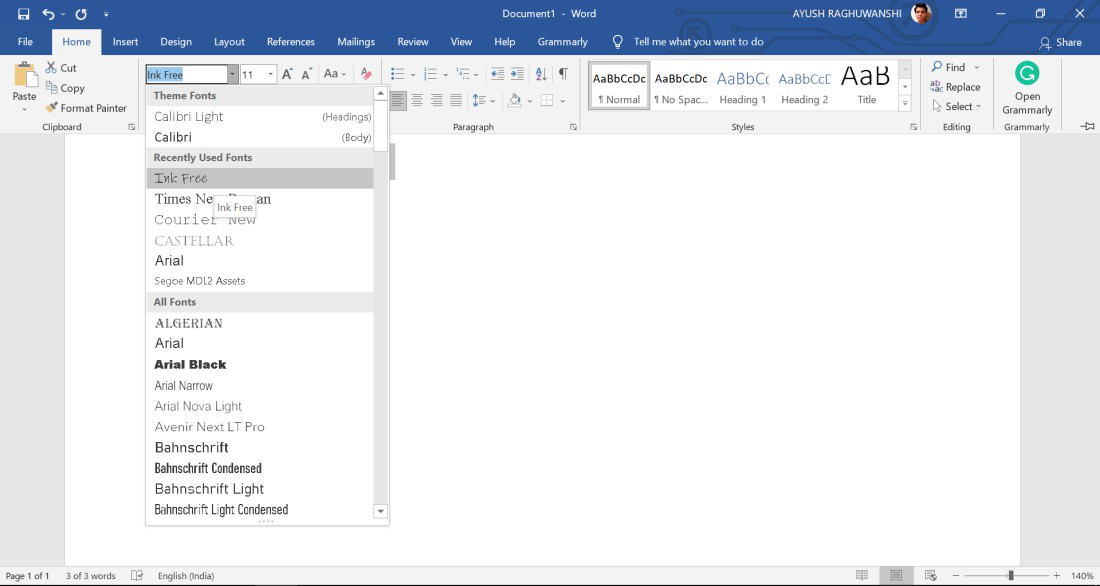
Result:

Font Style

Font Styles are used to change the Look ability of the text or give more emphasis on some texts in the Word Document. There are three types of font styles in MS Word: Bold, Italics, and Underline.

Steps to Apply Bold Font Style:

Step 1: Select the text you want to change the Font Style.

Step 2: Now, select the Font Style of your choice from the Font Style bar under the Home menu bar.

Result:

Steps to Apply Italics Font Style:

Step 1: Now, select the Font Style of your choice from the Font Style bar under the Home menu bar.

Result:

Steps to Apply Underline Font Style:

Step 1: Now, select the Font Style of your choice from the Font Style bar under the Home menu bar.

Result:

You could also use the shortcuts like:

CTRL+B for Bold

CTRL+I for Italics

CTRL+U for Underline

Font Color

Font Colors have wide use in real life when using the Word Document. Be it highlighting the main points of the document or want to convey some important information. There are multiple types of Font Colors available in MS Word-like: Red, Blue, Yellow, Orange, Light blue, etc.

Steps to Apply:

Step 1: Select the text you want to change the Font Color.

Step 2: Now, select the Font Color of your choice from the Font Color bar under the Home menu bar.

Result:

Font Sizes are used to display the text in the Word Document larger or smaller according to our needs. We generally display a heading with a Font Size of 15, Subheadings with a Font Size of 14 or 13, and paragraphs with a Font Size of 12. Many Font Sizes are available in MS Word-like: 8, 9, 10, 11, 12, 14, 16, etc.

Steps to Apply:

Step 1: Select the text you want to change the Font Size.

Step 2: Now, select the Font Size of your choice from the Font Size bar under the Home menu bar.

Result:

Text Highlight Color

As the name itself suggests, the Text Highlight Color is used to highlight text in the Word Document. There are many Text Highlight Colors available in MS Word-like: Yellow, Bright Green, Turquoise, Pink, Red, etc.

Steps to Apply:

Step 1: Select the text you want to change the Highlight Colors.

Step 2: Now, select the Color of your choice from the Text Highlight Color bar under the Home menu bar.

Result:

Clear Formats

MS Word provides a feature to clear the pre-formatted text. When we copy some text or information from somewhere it has some formatting applied already, so to remove it and use it according to our need in our Word Document we have to clear the Formatting.

Steps to Apply:

Step 1: Select the text you want to clear the formatting.

Step 2: Now, select the Clear All Formatting bar under the Home menu bar.

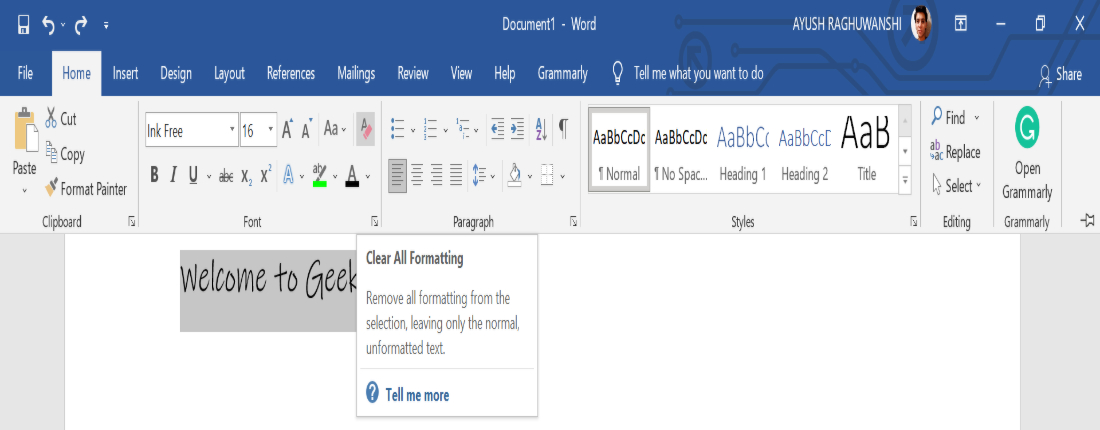
Result:

Change Case

Change Case is used to display the text in the way we want in our Word Document. There are five types of Change Cases available in MS Word-like: Sentence case, Lowercase, Uppercase, Capitalize each word, and toggle case.

Steps to Apply:

Step 1: Select the text you want to change the Case.