Applications of Trigonometry in Real Life are manyfold and can be encountered in daily life too. Trigonometry has a lot of real-life applications of trigonometry such as in astronomy to calculate the distance between planets and stars. Other than that, one application of trigonometry is the calculation of the height and distance of various objects in the real world.
In this article, we’ll learn about the uses and applications of trigonometry and some basic concepts of trigonometry.

What is Trigonometry?
Trigonometry is the branch of mathematics that deals with the study of relationships between the sides and angles of a triangle. In trigonometry, there are six trigonometry ratios such as sine, cosine, tan, sec, cosec, and cot. Before understanding the application of Trigonometry, we need to understand some basic terms such as
- Line of Sight
- Angle of Elevation
- Angle of Depression
Line of Sight
Consider a person looking at the top of the light tower as in the below figure:
.webp)
Line of Sight – Trigonometry
In this figure, the line DE drawn from the eye of the boy to the top of the tower is called a Line of Sight.
Angle of Elevation
Consider a person looking at the top of the light tower as in the below figure:
.webp)
Angle of Elevation – Trigonometry
The angle between the line of sight and the horizontal level at the eye of the boy, ΔCDA or ∠D, is called the angle of elevation.
When we measure the angle of elevation, the observer should raise their head and look above the horizontal level.

Measure of Angle of Elevation
Here if one wants to calculate the height of the tower without actually measuring it then what and how much information is required? The following detail is necessary to find out the height of the tower without measuring it:
- Distance, AB or CD, between the tower and the point where the boy standing.
- The angle of elevation, ∠EDC, of the top of the tower.
- The height of the boy DA.
In ΔCDE, the known ∠D is the opposite of the side CE, and it is known that the side CD. So here is the trigonometry ratio, that can be used to apply all these three quantities. Determine tan D or cot D as their ratio involves CD and CE.
While calculating the length of the tower or any other object, one should keep in mind the length of the boy to add in the result get from the trigonometry ratio. By the following example, this concept will more clear.
Angle of Depression
Now consider a situation as in given figure 4, a person is looking towards a ball from a balcony. Its line of sight is below the horizontal level. The angle between the line of sight and the horizontal level is called the angle of depression.
.webp)
Angle of Depression – Trigonometry
Thus, the angle of depression of the point on the object is the angle between the horizontal level and line of sight when the point is the below horizontal level

Measure of Angle of Depression
In the above figure, the person at point C, is looking towards the ball at B. CB is the line of sight and AC is the height of the balcony.
In ΔBCD, ∠BCD is the angle of depression of point B. Here is the height of the balcony AC = BD and the distance of the ball from the ground foot of the building AB = CD. According to the given data, the trigonometry ratio can be used as it can involve both known and unknown quantities.
Applications of Trigonometry in Real Life
There are various applications of trigonometry and some of the common applications of trigonometry are:
Trigonometry to Measure Height
The basic use or application of trigonometry is the measure of height. We use the concept of trigonometry to measure the height and distance between two objects by measuring the angles between these objects. We can easily find the height of an object if we know the distance between any point and the foot of the building and the angle of elevation or the depression of that point from the building.
Example: A person standing 20 meters away from the base of a building observes that the angle of elevation to the top of the building is 45 degrees. Determine the height of the building.
Solution:
Given: Distance from the base of the building to the observer, d = 20 metres Angle of elevation, θ = 45 degrees
Step-by-step Solution:
- Use the tangent function to relate the angle of elevation to the height of the building:
tangent (θ) = height of building / distance from observer to base of building - Substitute the given values into the tangent function:
tangent( 45°) = height of building / 20 - Simplify using the tangent of 45 degrees:
1 = height of building / 20 - Solve for the height of the building: height of building = 20 metres
Therefore, the height of the building is 20 meters.
Trigonometry in Aviation
We use trigonometry in aviation for measuring the height and speed of any flying objects such as Airplanes and missiles. The exact position of the airplane and other flying objects can be measured if we are given its height and the angle of elevation.
Trigonometry in Navigation
Trigonometry is widely used in the navigation of ships and others we can easily find the position of our ship in the ocean with the help of stars and the knowledge of trigonometry and angles.
Trigonometry in Astronomy
Trigonometry is widely used in astronomy to find the distances and positions of the stars and other heavenly bodies. We can measure the angle of various heavenly bodies from the Earth by knowing the time taken by the light from that body to reach the Earth’s surface and the speed of light we can find its position in space using trigonometry.
Other Uses of Trigonometry
The other uses of trigonometry are discussed below,
- It is used in criminology to study crime scenes.
- It is used by marine biologists to study the depth of oceans and others.
- It is used to study waves and their properties.
People Also Read:
Applications of Trigonometry – Solved Examples
Problem 1: A pole stands vertically on the plane. From a point on the plane, which is 12 m away from the foot of the pole, the angle of elevation of the top of the pole is 30° Find the height of the pole.
Solution:
First, draw a simple diagram of the given problem as below:

In this figure, BC represents the height of the electric pole and ∠CAB or ∠A represents the angle of the elevation of the top of the tower. In ΔABC, ∠CAB is the right angle and AB = 12 m. In ΔABC, CB is needed to be determined i.e. the height of the pole.
To solve the given problem, use trigonometry ratio tan A or cot A as they involve given sides in ratios.
Now,
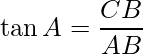
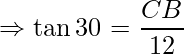
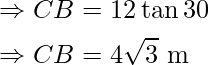
Hence, the height of the poll is 4√3.
Problem 2: A boy sees two clouds from a certain point. The angle of the elevation of the clouds are 30° and 45°. If the height of the clouds from the ground surface is the same and the distance between the clouds is 300 m then find out the height of the cloud.
Solution:
First, draw a simple diagram of the given problem as below.

In this figure, CE and BD represents the height of the clouds and ∠DAB and ∠EAC represents the angle of the elevation of the clouds at point A. In ΔABD, ∠DBA is the right angle, if the height of cloud BD is h then using trigonometry ratio tan A
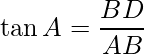
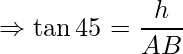
⇒ AB = h (Since, tan 45° = 1)
In ΔACE, ∠ACE is the right angle, if the height of cloud CE is h then using trigonometry ratio as:

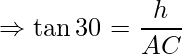
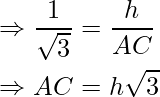
⇒ AC = h√3
From the above figure 4,
AC = AB + BC
Given: BC = 300.
Therefore,
h√3 = h + 300

Hence, the height of the cloud is 410.96 m.
Problem 3: The angle of elevation of the bird, who was sitting on a tree, from a point on the ground, which is 60 m away from the foot of the tree, is 60°. Find the height of the tree. (Take √3 = 1.73).
Solution:
First draw a simple diagram of the given problem as below:

In above figure, AB represents the distance between the ground point and foot of the tree, i.e. 60 m. BC is the height of the tree, let’s assume h.
In ΔABC, ∠ABC is the right angle, and the angle of the elevation is ∠B i.e. 60°.
Using trigonometry ratio tan A,
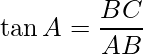

Hence, the height of the tree is 103.8 m.
Problem 4: The angle of depression of a bike, standing in a park, from the top of a 45 m high building, is 30°. What is the distance of the bike from the base of the building (in m)?
Solution:
Below is a simple diagram of the given problem.

In above figure, AB represents the distance between the base of the building and the bike. AC is the height of the building, i.e. 45 m.
In ΔBCD, ∠BCD is the right angle and the angle of the depression is ∠C i.e. 30°. Using trigonometry ratio tan C in ΔBCD.
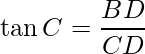
Here AC = BD and AB = CD.
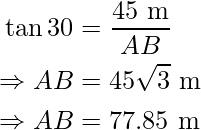
Hence, the distance between the base of building and the bike is 77.85 m.
Problem 5: An electrician needs to repair an electric fault to solve the power supply issue in a village. The height of the electric pole, on which the fault exists, is 7 m. He wants to reach a point below 1.5 m from the top of the pole to repair the fault. What length of the ladder he should use to reach the required position if the ladder is inclined at 60° to the horizontal? Also, find how far the ladder he should place from the foot of the pole (Take √3 = 1.73).
Solution:
First, Draw a basic diagram of the given problem as below:
In this figure, BC is the ladder, AD is the total length of the pole, Point C is the where electrician wants to reach.

As given CD = 1.5 m and AD = 7 m.
Therefore,
AC = AD – CD
⇒ AC = 7 – 1.5 m
⇒ AC = 5.5 m
In ΔABC, ∠B is 60° and ∠A is right angle,
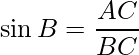
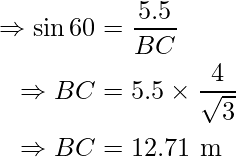
And, in ΔABC,
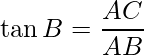
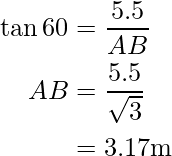
Hence, the length of the ladder BC is 12.71 m and the distance between ladder and foot of the pole AB is 3.17 m.
Problem 6: The angle of elevation of a cloud from a point, which is somewhere on the surface of the water of a lake, is 30°. The angle of depression of the shadow of a cloud in the water of the lake from the same point is 60°. If the height of the cloud is 75 m then find the depth of the shadow. (Take √3 = 1.73).
Solution:
First, draw a basic diagram of the given problem as below:

In this figure, AB is the water surface of the lake. Points C and D represent the cloud and its shadow respectively. ∠ABC and ∠ABD are the right angles. BC is the height of the cloud, i.e. 75 m and BD is the depth of the shadow. ∠BAC and ∠BAD are the angle of elevation and the angle of the depression, i.e. 30° and 60°.
In ΔABC,
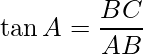
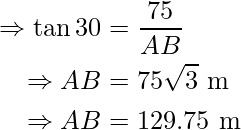
Now in ΔABD,
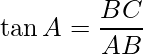

Hence, the depth of the shadow is 224.46 m.
Problem 7: Consider the following diagram:

If the √ACB is the right angle find the AB and CD (Take √3 = 1.73).
Solution:
In ΔACD, use the trigonometry ratio sin A,
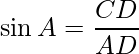

And,
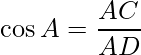

In ΔBCD, use the trigonometry ratio  ,
,
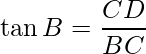
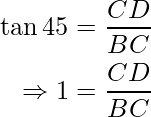
⇒ BC = CD = 2.5 m
From the given figure:
AC = AB + BC
⇒ AB = 4.33 m – 2.5 m
⇒ AB =1.83 m
Hence, AB = 1.83 m and CD = 2.5 m.
Problem 8: A 1.5 m tall boy is looking toward two buildings. Both buildings have a height of 12 m. The elevation angle of the top of the buildings is 45° and 60°. Find the distance between the two buildings and the distance of the boy from the near building.
Solution:
A simple diagram of the given problem is drawn below
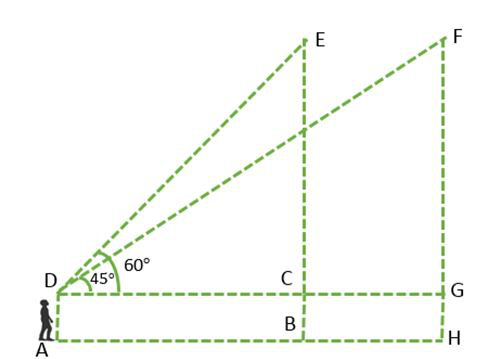
Figure 6
In the above figure, CB and GH represent the two buildings, CG is the distance between the two buildings, CD and GD is the distance between the boy and foot of the buildings of EB and FH respectively.
In ΔCDE and ΔFDG,
EC = FG = EB – AD (Since, AD = CB = GH)
⇒ EC = FG = 12 m – 1.5 m
⇒ EC = FG = 10.5 m
In ΔCDE, ∠CDE is equal to  and ∠DCE is the right angle.
and ∠DCE is the right angle.
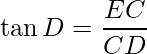
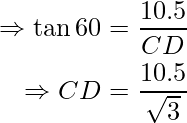
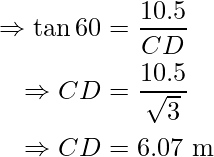
In ΔFDG, ∠FDG is  and ∠FGD is right angle.
and ∠FGD is right angle.
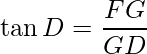
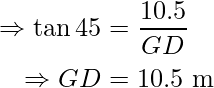
The distance between the buildings is:
CG = GD – CD
⇒ CG = 10.5 m – 6.07 m
⇒ CG = 4.43 m
Hence, the distance between the buildings CG is 4.43 m and the distance between the boy and the foot of the near building CD is 6.07 m.
FAQs on Applications of Trigonometry in Real Life
Define Trigonometry.
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles.
What are Basic Trigonometric Ratios?
The basic trigonometric ratios are sine, cosine, and tangent. These ratios relate the sides of a right triangle to its angles.
What is the Sine Ratio?
The sine ratio is defined as the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right triangle.
What is the Cosine Ratio?
The cosine ratio is defined as the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle.
What is the Tangent Ratio?
The tangent ratio is defined as the ratio of the length of the side opposite an angle to the length of the adjacent side in a right triangle.
What are the Reciprocal Trigonometric Ratios?
The reciprocal trigonometric ratios are cosecant, secant, and cotangent. These ratios are the reciprocals of the sine, cosine, and tangent ratios, respectively.
What are some Real-life Applications of Trigonometry?
Trigonometry has many practical applications in fields such as engineering, architecture, physics, and navigation. It can be used to calculate distances, angles, heights, and other geometric quantities in real-world situations.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...