Applications of Power Rule
Last Updated :
16 Jun, 2021
Differentiation of a function is breaking up the function into a smaller and much simpler version of itself. Derivative of any function is differentiating it with respect to the variable present in it, in easier words, derivatives are the rate of change of any function with respect to the variable present in it. For instance, when a car is driven too fast, the police take action, but how do they know that the speed limit is crossed? What is speed? Speed is nothing but the derivative of the distance with respect to time, if a car is too fast, it is covering more distance per unit of time and hence, has more speed.
This is the most basic example of how derivatives work. A function can be really complex and therefore, some rules are defined for them, one of those rules is the power rule, let’s look into it in more detail.
Power Rule
Power rule as the name suggests is defined for functions with exponents present, like the square of the variable or cube of the function, etc. Power rule is the most common and basic rule to learn in derivative but equally important as it is used in most complex functions too.
In order to use the Power Rule, take the exponent and multiply it with the coefficient of the variable and decrease the exponent by 1.
The given function is, axn
The derivative of this function using power rule will be,
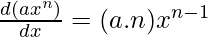
Let’s walk through different types of functions and see how the power rule works on each of them, keep in mind that the rule remains the same in all of them,
Differentiating Polynomials
The above general formula is defined for a polynomial and any polynomial (monomial, binomial, etc) can be differentiated with a power rule.
Example: Find the derivative of the functions given below,
- f(x) = 5x6
- f(y) = 60y100
- f(z) = xy9z3
Solution:
(i) f(x)= 5x6
Differentiating f(x) w.r.t. x,
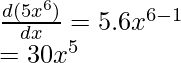
(ii) f(y)= 60y100
Differentiating f(y) w.r.t. y,
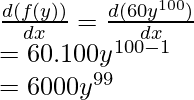
(iii) f(z)= xy9z3
Differentiating f(z) w.r.t. z, here one important thing to keep in mind is that the function has z as a variable, therefore, x and y are treated as a constant.
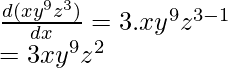
Note: Power rule can be applied for any function with some power, typically looks like xn where n is the power or exponent. A function in the form of axn are known as Power functions.
Can the Power rule be applied to the functions where power is not visible?
YES. Every variable has some power, even in the absence of variables, a variable can be added with a power 0 and then the power rule is applied.
Let’s understand the concept of applying power rule to such functions in more detail,
Differentiating Negative numbers
Suppose a function has negative power or the function is given in form of a fraction (basically, negative power is present on the function, in such a case,
- Convert the fraction in respective power form.
- Differentiate the function using power rule.
- Convert it back to the fraction form.
Example: Find the derivative of the function, f(x) = 1/x4.
Solution:
f(x) = 1/x4
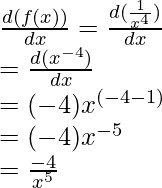
Differentiating Radicals and fractional powers
In order to differentiate Radicals or fractional powers, follow the steps,
- Convert Radicals in Power form.
- Apply the derivative.
- Convert back in radical form.
Example: Find the derivative of the function, f(x) = 3√x
Solution:
f(x) = 3√x
Differentiating f(x) w.r.t. x,
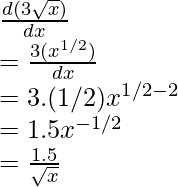
Differentiating a Constant
The derivative of a constant is 0. Even a constant can be differentiated with the help of Power rule, since adding a variable with a power of 0 will not affect the function/constant. Then, with the help of the same variable, use power rule to differentiate the function.
Example: Find the derivative of the function, f(x) = 8.
Solution:
f(x) = 8
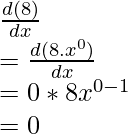
Sample Problems
Question 1: Find the derivative of the function with respect to x, f(x) = 100x100
Solution:
f(x) = 100 x100
Differentiating w.r.t. x,
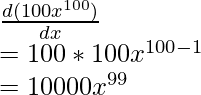
Question 2: Find the derivative of the function given below,
f(x)= 3x2+ 5x+ 9
Solution:
f(x)= 3x2+ 5x+ 9
Differentiating w.r.t. x,
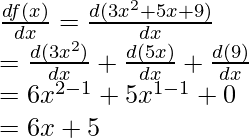
Question 3: Find the derivative of the function,
f(x)= 30x7+ 9√x+ 66
Solution:
f(x)= 30x7+9√x+66
Differentiating w.r.t. x,
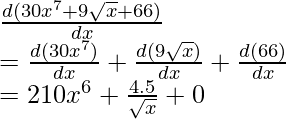
Question 4: Find the derivative of the given functions,
- f(x)=9
- f(x)=x
- f(x)=z
- f(x)=1/x
- f(x)=√x
Solution:
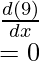
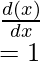
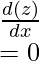
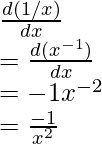
Question 5: Find the derivative of the function given below,
f(x)= 6√x+ 7/x5+ yx
Solution:
f(x)= 6√x+ 7/x5+ yx
Differentiating w.r.t. x,
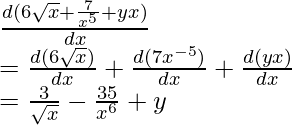
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...