Applications of Catalan Numbers
Last Updated :
01 Feb, 2023
Background :
Catalan numbers are defined using below formula:
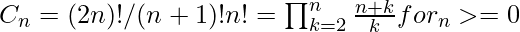
Catalan numbers can also be defined using following recursive formula.
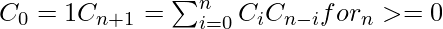
The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
Refer this for implementation of n’th Catalan Number.
Applications :
- Number of possible Binary Search Trees with n keys.
- Number of expressions containing n pairs of parentheses which are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
- Number of ways a convex polygon of n+2 sides can split into triangles by connecting vertices.

- Number of full binary trees (A rooted binary tree is full if every vertex has either two children or no children) with n+1 leaves.
- Number of different Unlabeled Binary Trees can be there with n nodes.
- The number of paths with 2n steps on a rectangular grid from bottom left, i.e., (n-1, 0) to top right (0, n-1) that do not cross above the main diagonal.

- Number of ways to insert n pairs of parentheses in a word of n+1 letters, e.g., for n=2 there are 2 ways: ((ab)c) or (a(bc)). For n=3 there are 5 ways, ((ab)(cd)), (((ab)c)d), ((a(bc))d), (a((bc)d)), (a(b(cd))).
- Number of noncrossing partitions of the set {1, …, 2n} in which every block is of size 2. A partition is noncrossing if and only if in its planar diagram, the blocks are disjoint (i.e. don’t cross). For example, below two are crossing and non-crossing partitions of {1, 2, 3, 4, 5, 6, 7, 8, 9}. The partition {{1, 5, 7}, {2, 3, 8}, {4, 6}, {9}} is crossing and partition {{1, 5, 7}, {2, 3}, {4}, {6}, {8, 9}} is non-crossing.

- Number of Dyck words of length 2n. A Dyck word is a string consisting of n X’s and n Y’s such that no initial segment of the string has more Y’s than X’s. For example, the following are the Dyck words of length 6: XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.
- Number of ways to tile a stairstep shape of height n with n rectangles. The following figure illustrates the case n = 4:

- Number of ways to connect the points on a circle disjoint chords. This is similar to point 3 above.
- Number of ways to form a “mountain ranges” with n upstrokes and n down-strokes that all stay above the original line.The mountain range interpretation is that the mountains will never go below the horizon.

- Number of stack-sortable permutations of {1, …, n}. A permutation w is called stack-sortable if S(w) = (1, …, n), where S(w) is defined recursively as follows: write w = unv where n is the largest element in w and u and v are shorter sequences, and set S(w) = S(u)S(v)n, with S being the identity for one-element sequences.
- Number of permutations of {1, …, n} that avoid the pattern 123 (or any of the other patterns of length 3); that is, the number of permutations with no three-term increasing subsequence. For n = 3, these permutations are 132, 213, 231, 312 and 321. For n = 4, they are 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 and 4321
Sources:
- https://en.wikipedia.org/wiki/Catalan_number
- http://mathworld.wolfram.com/CatalanNumber.html
- http://www-groups.dcs.st-and.ac.uk/history/Miscellaneous/CatalanNumbers/catalan.html
- http://www.mhhe.com/math/advmath/rosen/r5/instructor/applications/ch07.pdf
- https://oeis.org/A000108
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...