Apothem of a n-sided regular polygon
Last Updated :
22 Jun, 2022
Given here the side length a of a regular n-sided polygon, the task is to find the length of its Apothem.
Apothem is the line drawn from the center of the polygon that is perpendicular to one of its sides.
Examples:
Input a = 9, n = 6
Output: 7.79424
Input: a = 8, n = 7
Output: 8.30609
Approach:
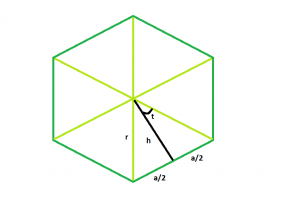
In the figure, we see the polygon can be divided into n equal triangles.
Looking into one of the triangles, we see the whole angle at the centre can be divided into = 360/n
So, angle t = 180/n
now, tan t = a/2h
So, h = a/(2*tan t)
here, h is the apothem,
so, apothem = a/(2*tan(180/n))
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
float polyapothem(float n, float a)
{
if (a < 0 && n < 0)
return -1;
return a / (2 * tan((180 / n) * 3.14159 / 180));
}
int main()
{
float a = 9, n = 6;
cout << polyapothem(n, a) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
double polyapothem(double n, double a)
{
if (a < 0 && n < 0)
return -1;
return (a / (2 * java.lang.Math.tan((180 / n)
* 3.14159 / 180)));
}
public static void main(String args[])
{
double a = 9, n = 6;
GFG g=new GFG();
System.out.println(g.polyapothem(n, a));
}
}
|
Python3
from math import tan
def polyapothem(n, a):
if (a < 0 and n < 0):
return -1
return a / (2 * tan((180 / n) *
3.14159 / 180))
if __name__ == '__main__':
a = 9
n = 6
print('{0:.6}'.format(polyapothem(n, a)))
|
C#
using System;
class GFG
{
static double polyapothem(double n,
double a)
{
if (a < 0 && n < 0)
return -1;
return (a / (2 * Math.Tan((180 / n) *
3.14159 / 180)));
}
public static void Main()
{
double a = 9, n = 6;
Console.WriteLine(Math.Round(polyapothem(n, a), 4));
}
}
|
PHP
<?php
function polyapothem($n, $a)
{
if ($a < 0 && $n < 0)
return -1;
return $a / (2 * tan((180 / $n) *
3.14159 / 180));
}
$a = 9; $n = 6;
echo polyapothem($n, $a) . "\n";
?>
|
Javascript
<script>
function polyapothem(n , a)
{
if (a < 0 && n < 0)
return -1;
return (a / (2 * Math.tan((180 / n)
* 3.14159 / 180)));
}
var a = 9, n = 6;
document.write(polyapothem(n, a).toFixed(5));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...