ANN – Bidirectional Associative Memory (BAM)
Last Updated :
10 Jul, 2020
Bidirectional Associative Memory (BAM) is a
supervised learning model in Artificial Neural Network. This is
hetero-associative memory, for an input pattern, it returns another pattern which is potentially of a different size. This phenomenon is very similar to the human brain. Human memory is necessarily associative. It uses a chain of mental associations to recover a lost memory like associations of faces with names, in exam questions with answers, etc.
In such memory associations for one type of object with another, a
Recurrent Neural Network (RNN) is needed to receive a pattern of one set of neurons as an input and generate a related, but different, output pattern of another set of neurons.
Why BAM is required?
The main objective to introduce such a network model is to store hetero-associative pattern pairs.
This is used to retrieve a pattern given a noisy or incomplete pattern.
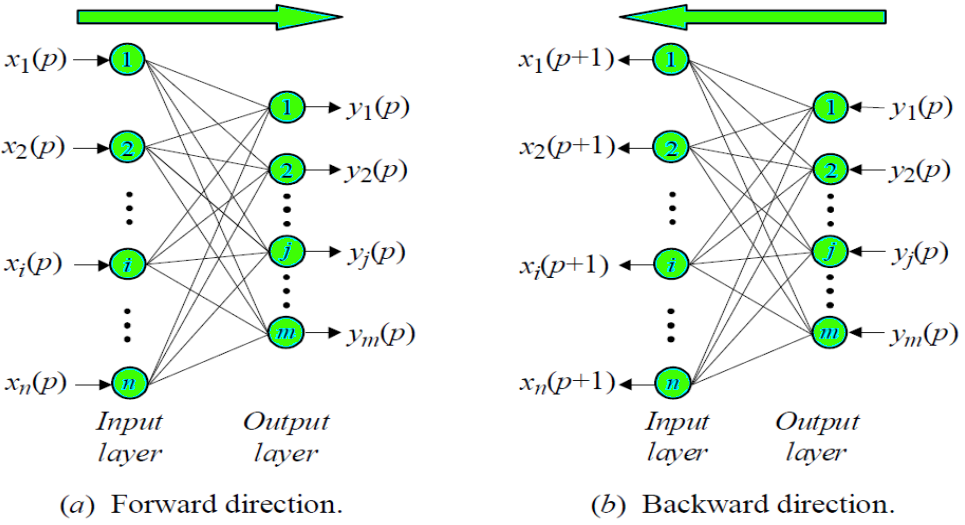
BAM Architecture:
When BAM accepts an input of
n-dimensional vector
X from set
A then the model recalls
m-dimensional vector
Y from set
B. Similarly when
Y is treated as input, the BAM recalls
X.
 Algorithm:
Algorithm:
- Storage (Learning): In this learning step of BAM, weight matrix is calculated between M pairs of patterns (fundamental memories) are stored in the synaptic weights of the network following the equation
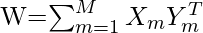
- Testing: We have to check that the BAM recalls perfectly
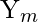 for corresponding
for corresponding 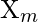 and recalls
and recalls 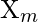 for corresponding
for corresponding 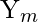 . Using,
. Using,
![Rendered by QuickLaTeX.com \[Y_{m}=\operatorname{sign}\left(W^{T} X_{m}\right), \quad m=1.2, \ldots, M\]\[X_{m}=\operatorname{sign}\left(W Y_{m}\right), \quad m=1.2, \ldots, M\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f370d7cbc5335de9eadce33a8080bf45_l3.png)
All pairs should be recalled accordingly.
- Retrieval: For an unknown vector X (a corrupted or incomplete version of a pattern from set A or B) to the BAM and retrieve a previously stored association:
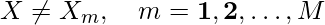
- Initialize the BAM:
![Rendered by QuickLaTeX.com \[X(0)=X, \quad p=0\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9e37ae44e2f22fc28d38c6c3f7ba570b_l3.png)
- Calculate the BAM output at iteration
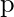 :
: ![Rendered by QuickLaTeX.com \[Y(p)=\operatorname{sign}\left[W^{T} X(p)\right]\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d94f969dc90ba3edaf05946c6f674df2_l3.png)
- Update the input vector
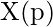 :
: ![Rendered by QuickLaTeX.com \[X(p+1)=\operatorname{sign}[W Y(p)]\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b89712bcea8306c42874b8ab999cc354_l3.png)
- Repeat the iteration until convergence, when input and output remain unchanged.
Limitations of BAM:
- Storage capacity of the BAM: In the BAM, stored number of associations should not be exceeded the number of neurons in the smaller layer.
- Incorrect convergence: Always the closest association may not be produced by BAM.
Share your thoughts in the comments
Please Login to comment...