Angular Sweep (Maximum points that can be enclosed in a circle of given radius)
Last Updated :
28 Mar, 2024
Given ‘n’ points on the 2-D plane, find the maximum number of points that can be enclosed by a fixed-radius circle of radius ‘R’.
Note: The point is considered to be inside the circle even when it lies on the circumference.
Examples:
Input: R = 1
points[] = {(6.47634, 7.69628), (5.16828 4.79915),
(6.69533 6.20378)}
Output: 2
The maximum number of points is 2
Input: R = 1
points[] = {(6.65128, 5.47490), (6.42743, 6.26189)
(6.35864, 4.61611), (6.59020 4.54228), (4.43967 5.70059)
(4.38226, 5.70536), (5.50755 6.18163), (7.41971 6.13668)
(6.71936, 3.04496), (5.61832, 4.23857), (5.99424, 4.29328)
(5.60961, 4.32998), (6.82242, 5.79683), (5.44693, 3.82724) |
(6.70906, 3.65736), (7.89087, 5.68000), (6.23300, 4.59530)
(5.92401, 4.92329), (6.24168, 3.81389), (6.22671, 3.62210)}
Output: 11
The maximum number of points is 11
Naive Algorithm:
For an arbitrary pair of points in the given set (say A and B), construct the circles with radius ‘R’ that touches both the points. There are maximum 2 such possible circles. As we can see here maximum possible circles is for CASE 1 i.e. 2.

- For each of the constructed circle, check for each point in the set if it lies inside the circle or not.
- The circle with maximum number of points enclosed is returned.
Time Complexity: There are nC2 pair of points corresponding to which we can have 2nC2 circles at maximum. For each circle, (n-2) points have to be checked. This makes the naive algorithm O(n3).
Angular Sweep Algorithm:
By using Angular Sweep, we can solve this problem in O(n2log n). The basic logical idea of this algorithm is described below.
We pick an arbitrary point P from the given set. We then rotate a circle with fixed-radius ‘R’ about the point P. During the entire rotation P lies on the circumference of the circle and we maintain a count of the number of points in the circle at a given value of ? where the parameter ? determines the angle of rotation. The state of a circle can thus be determined by a single parameter ? because the radius is fixed.
We can also see that the value of the count maintained will change only when a point from the set enters or exits the circle.
 In the given diagram, C1 is the circle with ? = 0 and C2 is the circle constructed when we rotate the circle at a general value of ?.
In the given diagram, C1 is the circle with ? = 0 and C2 is the circle constructed when we rotate the circle at a general value of ?.
After this, the problem reduces to, how to maintain the value of count.
For any given point except P (say Q), we can easily calculate the value of ? for which it enters the circle (Let it be ?) and the value of ? for which it exits the circle (Let it be ?).
We have angles A and B defined as under,
- A is the angle between PQ and the X-Axis.
- B is the angle between PC and PQ where C is the centre of the circle.
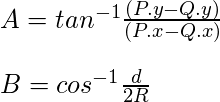
where, x and y represent the coordinates of a point and ‘d’ is the distance between P and Q.
Now, from the diagrams we can see that,
? = A-B
? = A+B
(Note: All angles are w.r.t. to X-Axis. Thus, it becomes ‘A-B’ and not ‘B-A’).
When Q enters the circle

When Q exits the circle

We can calculate angles A and B for all points excluding P. Once these angles are found, we sort them and then traverse them in increasing order. Now we maintain a counter which tells us how many points are inside the circle at a particular moment.
Count will change only when a point enters the circle or exits it. In case we find an entry angle we increase the counter by 1 and in case we find an exit angle we decrease the counter by 1. The check that the angle is entry or exit can be easily realised using a flag.
Proceeding like this, the counter always gives us a valid value for the number of points inside the circle in a particular state.
Important Note: The points which have ‘d’>2R do not have to be considered because they will never enter or exit the circle.
The angular sweep algorithm can be described as:
- Calculate the distance between every pair of nC2 points and store them.
- For an arbitrary point (say P), get the maximum number of points that can lie inside the circle rotated about P using the getPointsInside() function.
- The maximum of all values returned will be the final answer.
Below is the implementation of the above approach:
CPP
// C++ program to find the maximum number of
// points that can be enclosed by a fixed-radius
// circle
#include <bits/stdc++.h>
using namespace std;
const int MAX_POINTS = 500;
// complex class which is available in STL has
// been used to implement points. This helps to
// ensure greater functionality easily
typedef complex<double> Point;
Point arr[MAX_POINTS];
double dis[MAX_POINTS][MAX_POINTS];
// This function returns the maximum points that
// can lie inside the circle of radius 'r' being
// rotated about point 'i'
bool mycompare(pair<double,bool> A, pair<double,bool> B)
{
if(A.first<B.first)
return true;
else if(A.first>B.first)
return false;
else
return (A.second==1);
}
int getPointsInside(int i, double r, int n)
{
// This vector stores alpha and beta and flag
// is marked true for alpha and false for beta
vector<pair<double, bool> > angles;
for (int j=0; j<n; j++)
{
if (i != j && dis[i][j] <= 2*r)
{
// acos returns the arc cosine of the complex
// used for cosine inverse
double B = acos(dis[i][j]/(2*r));
// arg returns the phase angle of the complex
double A = arg(arr[j]-arr[i]);
double alpha = A-B;
double beta = A+B;
angles.push_back(make_pair(alpha, true));
angles.push_back(make_pair(beta, false));
}
}
// angles vector is sorted and traversed
sort(angles.begin(), angles.end(), mycompare);
// count maintains the number of points inside
// the circle at certain value of theta
// res maintains the maximum of all count
int count = 1, res = 1;
vector<pair<double, bool> >::iterator it;
for (it=angles.begin(); it!=angles.end(); ++it)
{
// entry angle
if ((*it).second)
count++;
// exit angle
else
count--;
if (count > res)
res = count;
}
return res;
}
// Returns count of maximum points that can lie
// in a circle of radius r.
int maxPoints(Point arr[], int n, int r)
{
// dis array stores the distance between every
// pair of points
for (int i=0; i<n-1; i++)
for (int j=i+1; j<n; j++)
// abs gives the magnitude of the complex
// number and hence the distance between
// i and j
dis[i][j] = dis[j][i] = abs(arr[i]-arr[j]);
// This loop picks a point p
int ans = 0;
for (int i=0; i<n; i++)
// maximum number of points for point arr[i]
ans = max(ans, getPointsInside(i, r, n));
return ans;
}
// Driver code
int main()
{
Point arr[] = {Point(6.47634, 7.69628),
Point(5.16828, 4.79915),
Point(6.69533, 6.20378)};
int r = 1;
int n = sizeof(arr)/sizeof(arr[0]);
cout << "The maximum number of points are: "
<< maxPoints(arr, n, r);
return 0;
}
import java.util.*;
class MaximumPointsInCircle {
static final int MAX_POINTS = 500;
static Point[] arr = new Point[MAX_POINTS];
static double[][] dis = new double[MAX_POINTS][MAX_POINTS];
static class Point {
double x, y;
public Point(double x, double y) {
this.x = x;
this.y = y;
}
}
static int mycompare(AbstractMap.SimpleEntry<Double, Boolean> A, AbstractMap.SimpleEntry<Double, Boolean> B) {
if (A.getKey() < B.getKey())
return -1;
else if (A.getKey() > B.getKey())
return 1;
else
return (A.getValue() ? 1 : -1);
}
static int getPointsInside(int i, double r, int n) {
List<AbstractMap.SimpleEntry<Double, Boolean>> angles = new ArrayList<>();
for (int j = 0; j < n; j++) {
if (i != j && dis[i][j] <= 2 * r) {
double B = Math.acos(dis[i][j] / (2 * r));
double A = Math.atan2(arr[j].y - arr[i].y, arr[j].x - arr[i].x);
double alpha = A - B;
double beta = A + B;
angles.add(new AbstractMap.SimpleEntry<>(alpha, true));
angles.add(new AbstractMap.SimpleEntry<>(beta, false));
}
}
angles.sort((A, B) -> mycompare(A, B));
int count = 1, res = 1;
for (AbstractMap.SimpleEntry<Double, Boolean> angle : angles) {
if (angle.getValue())
count++;
else
count--;
if (count > res)
res = count;
}
return res;
}
static int maxPoints(Point[] arr, int n, int r) {
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
dis[i][j] = dis[j][i] = Math.hypot(arr[i].x - arr[j].x, arr[i].y - arr[j].y);
}
}
int ans = 0;
for (int i = 0; i < n; i++) {
ans = Math.max(ans, getPointsInside(i, r, n));
}
return ans;
}
public static void main(String[] args) {
arr[0] = new Point(6.47634, 7.69628);
arr[1] = new Point(5.16828, 4.79915);
arr[2] = new Point(6.69533, 6.20378);
int r = 1;
int n = 3;
System.out.println("The maximum number of points are: " + maxPoints(arr, n, r));
}
}
using System;
using System.Collections.Generic;
public struct Complex
{
public double Real;
public double Imaginary;
public Complex(double real, double imaginary)
{
Real = real;
Imaginary = imaginary;
}
public static Complex operator -(Complex a, Complex b)
{
return new Complex(a.Real - b.Real, a.Imaginary - b.Imaginary);
}
public static double Abs(Complex c)
{
return Math.Sqrt(c.Real * c.Real + c.Imaginary * c.Imaginary);
}
public static double Atan2(double y, double x)
{
return Math.Atan2(y, x);
}
}
public class Program
{
const int MAX_POINTS = 500;
// This function returns the maximum points that
// can lie inside the circle of radius 'r' being
// rotated about point 'i'
static int GetPointsInside(int i, double r, int n, Complex[] arr, double[,] dis)
{
// This list stores alpha and beta and flag
// is marked true for alpha and false for beta
List<(double, bool)> angles = new List<(double, bool)>();
for (int j = 0; j < n; j++)
{
if (i != j && dis[i, j] <= 2 * r)
{
// acos returns the arc cosine of the complex
// used for cosine inverse
double B = Math.Acos(dis[i, j] / (2 * r));
// arg returns the phase angle of the complex
double A = Complex.Atan2(arr[j].Imaginary - arr[i].Imaginary, arr[j].Real - arr[i].Real);
double alpha = A - B;
double beta = A + B;
angles.Add((alpha, true));
angles.Add((beta, false));
}
}
// angles list is sorted and traversed
angles.Sort(CompareAngles);
// count maintains the number of points inside
// the circle at certain value of theta
// res maintains the maximum of all count
int count = 1, res = 1;
foreach (var angle in angles)
{
// entry angle
if (angle.Item2)
count++;
// exit angle
else
count--;
if (count > res)
res = count;
}
return res;
}
// Returns count of maximum points that can lie
// in a circle of radius r.
static int MaxPoints(Complex[] arr, int n, int r)
{
// dis array stores the distance between every
// pair of points
double[,] dis = new double[n, n];
for (int i = 0; i < n - 1; i++)
for (int j = i + 1; j < n; j++)
// abs gives the magnitude of the complex
// number and hence the distance between
// i and j
dis[i, j] = dis[j, i] = Complex.Abs(arr[i] - arr[j]);
// This loop picks a point p
int ans = 0;
for (int i = 0; i < n; i++)
// maximum number of points for point arr[i]
ans = Math.Max(ans, GetPointsInside(i, r, n, arr, dis));
return ans;
}
// Custom comparer for sorting angles
static int CompareAngles((double, bool) A, (double, bool) B)
{
if (A.Item1 < B.Item1)
return -1;
else if (A.Item1 > B.Item1)
return 1;
else
return A.Item2.CompareTo(B.Item2);
}
// Driver code
public static void Main(string[] args)
{
Complex[] arr = {
new Complex(6.47634, 7.69628),
new Complex(5.16828, 4.79915),
new Complex(6.69533, 6.20378)
};
int r = 1;
int n = arr.Length;
Console.WriteLine("The maximum number of points are: " + MaxPoints(arr, n, r));
}
}
// JavaScript program to find the maximum number of
// points that can be enclosed by a fixed-radius
// circle
const MAX_POINTS = 500;
// complex class which has
// been used to implement points. This helps to
// ensure greater functionality easily
class Point {
constructor(x, y) {
this.x = x;
this.y = y;
}
subtract(other) {
return new Point(this.x - other.x, this.y - other.y);
}
magnitude() {
return Math.sqrt(this.x * this.x + this.y * this.y);
}
arg() {
return Math.atan2(this.y, this.x);
}
}
const arrPoints = [new Point(6.47634, 7.69628),
new Point(5.16828, 4.79915),
new Point(6.69533, 6.20378)];
const dis = new Array(MAX_POINTS).fill(0).map(() => new Array(MAX_POINTS).fill(0));
// This function returns the maximum points that
// can lie inside the circle of radius 'r' being
// rotated about point 'i'
function mycompare(A, B) {
if (A.first < B.first) {
return -1;
} else if (A.first > B.first) {
return 1;
} else {
return A.second == 1 ? -1 : 1;
}
}
function getPointsInside(i, r, n) {
// This vector stores alpha and beta and flag
// is marked true for alpha and false for beta
let angles = [];
for (let j = 0; j < n; j++) {
if (i != j && dis[i][j] <= 2 * r) {
// acos returns the arc cosine of the complex
// used for cosine inverse
let B = Math.acos(dis[i][j] / (2 * r));
// arg returns the phase angle of the complex
let A = arrPoints[j].subtract(arrPoints[i]).arg();
let alpha = A - B;
let beta = A + B;
angles.push([alpha, true]);
angles.push([beta, false]);
}
}
// angles vector is sorted and traversed
angles.sort(mycompare);
// count maintains the number of points inside
// the circle at certain value of theta
// res maintains the maximum of all count
let count = 1;
let res = 1;
for (let i = 0; i < angles.length; i++) {
// entry angle
if (angles[i][1]) {
count++;
}
// exit angle
else {
count--;
}
if (count > res) {
res = count;
}
}
return res;
}
// Returns count of maximum points that can lie
// in a circle of radius r.
function maxPoints(arrPoints, n, r) {
// dis array stores the distance between every
// pair of points
for (let i = 0; i < n - 1; i++) {
for (let j = i + 1; j < n; j++) {
// abs gives the magnitude of the complex
// number and hence the distance between
// i and j
dis[i][j] = dis[j][i] = arrPoints[i].subtract(arrPoints[j]).magnitude();
}
}
// This loop picks a point p
let ans = 0;
for (let i = 0; i < n; i++) {
// maximum number of points for point arr[i]
ans = Math.max(ans, getPointsInside(i, r, n));
}
return ans;
}
// Driver code
const n = arrPoints.length;
const r = 1;
console.log(`The maximum number of points are: ${maxPoints(arrPoints, n, r)}`);
// This Code is Contributed by Prasad Kandekar(prasad264)
# python program to find the maximum number of
# points that can be enclosed by a fixed-radius
# circle
import math
MAX_POINTS = 500
arr = [0] * MAX_POINTS
dis = [[0 for i in range(MAX_POINTS)] for j in range(MAX_POINTS)]
# This function returns the maximum points that
# can lie inside the circle of radius 'r' being
# rotated about point 'i'
def mycompare(A, B):
if A[0] < B[0]:
return True
elif A[0] > B[0]:
return False
else:
return A[1] == 1
def getPointsInside(i, r, n):
# This vector stores alpha and beta and flag
# is marked true for alpha and false for beta
angles = []
for j in range(n):
if i != j and dis[i][j] <= 2*r:
# acos returns the arc cosine of the complex
# used for cosine inverse
B = math.acos(dis[i][j]/(2*r))
# arg returns the phase angle of the complex
A = math.atan2(arr[j].imag - arr[i].imag, arr[j].real - arr[i].real)
alpha = A - B
beta = A + B
angles.append([alpha, True])
angles.append([beta, False])
# angles vector is sorted and traversed
angles.sort(key=lambda x: (x[0], x[1] == 1))
# count maintains the number of points inside
# the circle at certain value of theta
# res maintains the maximum of all count
count = 1
res = 1
for angle in angles:
# entry angle
if angle[1]:
count += 1
# exit angle
else:
count -= 1
res = max(res, count)
return res
# Returns count of maximum points that can lie
# in a circle of radius r.
def maxPoints(arr, n, r):
# dis array stores the distance between every
# pair of points
for i in range(n - 1):
for j in range(i + 1, n):
# abs gives the magnitude of the complex
# number and hence the distance between
# i and j
dis[i][j] = dis[j][i] = abs(arr[i] - arr[j])
# This loop picks a point p
ans = 0
for i in range(n):
# maximum number of points for point arr[i]
ans = max(ans, getPointsInside(i, r, n))
return ans
# Driver code
r = 1
arr = [complex(6.47634, 7.69628),
complex(5.16828, 4.79915),
complex(6.69533, 6.20378)]
n = len(arr)
print("The maximum number of points are:", maxPoints(arr, n, r))
# This Code is Contributed by Prasad Kandekar(prasad264)
Output:
The maximum number of points are: 2
Time Complexity: There are n points for which we call the function getPointsInside(). This function works on ‘n-1’ points for which we get 2*(n-1) size of the vector ‘angles’ (one entry angle and one exit angle). Now this ‘angles’ vector is sorted and traversed which gives complexity of the getPointsInside() function equal to O(nlogn). This makes the Angular Sweep Algorithm O(n2log n).
Space complexity: O(n) since using auxiliary space for vector
Related Resources: Using the complex class available in stl for implementing solutions to geometry problems.
http://codeforces.com/blog/entry/22175
Share your thoughts in the comments
Please Login to comment...