Angular Momentum

Angular Momentum is a kinematic characteristic of a system with one or more point masses. Angular momentum is sometimes called Rotational Momentum or Moment of Momentum, which is the rotational equivalent of linear momentum. It is an important physical quantity as it is conserved for a closed system and follows the Law of Conservation of Angular Momentum. Angular Momentum is equal to the product of the moment of inertia (I), and the angular velocity (ω), of an object in rotational motion. Angular Momentum is a vector quantity. The SI unit of angular momentum is Kg.m².s^-1

Let’s understand more concepts about angular momentum like What is Angular Momentum? Angular Momentum Formula, Unit and Dimensional formula of Angular Momentum, Spin, and Orbital angular momentum, the relation between torque and angular momentum, Law of Conservation of Angular Momentum, FAQs, and Examples of Angular Momentum.

What is Angular Momentum?

Angular Momentum is defined as the property of objects in rotational motion which is determined by the product of their moment of inertia and angular velocity.

When no external force is acting on a system of particles, the angular momentum in the system is found to be conserved. The total angular momentum of any composite system is equal to the sum of the angular momenta of each of its component elements, making angular momentum an extensive quantity. The total angular momentum for a continuous rigid body or fluid is the volume integral of the angular momentum density (angular momentum per unit volume in the limit as volume falls to zero).

The rotation and revolution of the Earth give one of the best examples of angular momentum. For example, the Earth’s everyday rotation around its axis represents spin angular momentum whereas its annual revolution around the Sun represents orbital angular momentum.

Angular Momentum Formula

The angular momentum for an object in rotational motion can happen in two ways. They must be, 

Angular Momentum of a Single Particle

Angular momentum can be experienced by a single particle when the object is accelerating around a fixed position. For example, in case of the earth and the sun. Earth is revolving around the sun in its orbit, where the sun is fixed at its position. 

Angular momentum, in that case is given by the formula,

where, 

•  is Angular Momentum
• r is Radius of Rotational Path
•  is Linear Momentum of Object

Angular Momentum for Extended Object

Angular momentum can be experienced by a point object when the object is rotating about a fixed position. For example, in case of the earth rotating at its axis.

Angular Momentum, in that case is given by the formula,

where, 

•  is Angular Momentum
• I is Rotational Inertia
•  is Angular Velocity of Object

Angular Momentum of a System of Particles

Angular Momentum of a system of particles is the vector sum of all the individual angular momentum of the single particles. The angular momentum of any particle is, l = r×p where r is the distance of particle form origin. and p is the linear momentum of the particle. The angular momentum of the system of n particle is,

L = l₁ + l₂ + l₃ +…+ l_n

Angular Momentum of a Rigid Body

Let’s assume that the object is made up of N particles with masses m₁, m₂,….m_N and perpendicular distances r₁, r₂,….r_N from the rotation axis. As the object rotates, all of these particles conduct UCM with the same angular speed ω but different line speeds v₁ = r₁ω, v₂ = r₂ω, … v_N = r_Nω.

Individual velocity directions, v₁, v₂, and so on, are along the tangents of their respective tracks. The initial particle’s linear momentum is p₁ = m₁v₁ = m₁r₁ω. It travels in the same direction as v₁. 

The magnitude of its angular momentum is consequently L₁ = p₁r₁ = m₁r₁²ω. Similarly, L₂ = m₂r₂²ω, L₃ = m₃r₃²ω, … L_N = m_Nr_N²ω.

All of these angular momenta are directed along the axis of rotation for a rigid body with a fixed axis of rotation, which may be determined using the right-hand thumb rule. Their magnitudes may be summed algebraically because they all have the same direction. As a result, the magnitude of the body’s angular momentum is given by,

L = m₁r₁²ω + m₂r₂²ω +….+ m_Nr_N²ω

∴ L = (m₁r₁² + m₂r₂² +…+ m_Nr_N²)ω = Iω

Thus, the angular momentum of any rigid body is, L = Iω

Unit of Angular Momentum

• SI unit of Angular Momentum is kg.m²/s. 
• CGS unit of Angular Momentum is g.cm²/s.
• Dimensional formula for Angular Momentum is, [ML²T^-1].

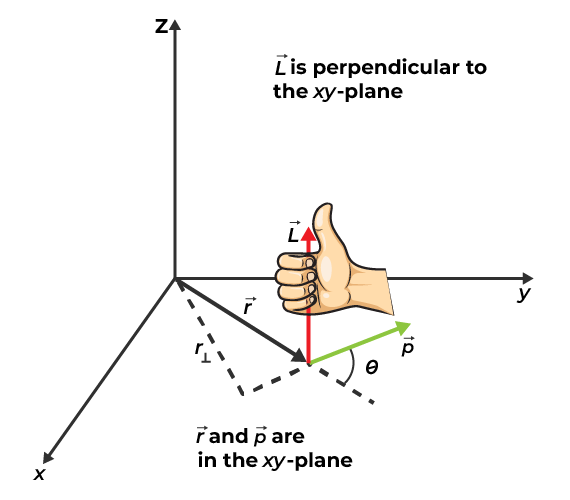
Right-Hand Thumb Rule

Direction of angular momentum can be determined by the right-hand thumb rule. If you position your right hand so that the fingers point in the direction of r. The curl is thus oriented in the direction of linear momentum (p). The outstretched thumb depicts the direction of angular momentum (L). 

Angular Momentum Quantum Number

Azimuthal quantum number or secondary quantum number is interchangeable with angular momentum quantum number. It is a quantum number that determines the angular momentum of an atomic orbital as well as its size and form. The most common value is between 0 and 1.

Angular Momentum and Moment of Inertia

Let’s assume that the object is made up of N particles with masses m₁, m₂,….m_N and perpendicular distances r₁, r₂,….r_N from the rotation axis. As the object rotates, all of these particles are in Uniform Circular Motion with the angular speed ω but their linear speeds are,

• v₁ = r₁ω
• v₂ = r₂ω
• v_N = r_Nω

Individual velocity directions, v₁, v₂, and so on, are along the tangents of their respective tracks. The initial particle’s linear momentum is p₁ = m₁v₁ = m₁r₁ω. It travels in the same direction as v₁. 

Magnitude of its angular momentum is, L₁ = p₁r₁ = m₁r₁²ω

Similarly, L₂ = m₂r₂²ω, L₃ = m₃r₃²ω, … L_N = m_Nr_N²ω

All of these angular momenta are directed along the axis of rotation for a rigid body with a fixed axis of rotation, which may be determined using the right-hand thumb rule. Their magnitudes may be summed algebraically because they all have the same direction. As a result, the magnitude of the body’s angular momentum is given by,

L = m₁r₁²ω + m₂r₂²ω +….+ m_Nr_N²ω

L = (m₁r₁² + m₂r₂² +…+ m_Nr_N²)ω = Iω

Moment of Inertia of body around the given axis of rotation is,

• I = m₁r₁² + m₂r₂² +…+ m_Nr_N²

If the moment of inertia I replace mass, the angular momentum statement L = Iω is comparable to the linear momentum expression p = mv, which is its physical significance.

Examples of Angular Momentum

Various examples where the concept of Angular Momentum is,

Gyroscope

To retain its orientation, a gyroscope uses the angular momentum principle. It works with a three-degree-of-freedom spinning wheel. It locks on to the orientation when turned at a rapid speed and will not stray from it. This is useful in space applications where controlling the attitude of a spacecraft is critical.

Ice-Skater

When ice skaters start a spin, their hands and legs are spread wide apart from their body’s center. They put their hands and legs closer to their bodies when spinning requires a higher angular velocity. They spin faster as a result of the conservation of angular momentum.

Law of Conservation of Angular Momentum

Everyone has seen the conservation of linear momentum, which states that in the absence of an external unbalanced force, the linear momentum of an isolated system is conserved. In rotational dynamics, torque and angular momentum are similar to force and linear momentum, as previously stated. With the right modifications, this can be turned into angular momentum conservation.

Angular momentum is given by the formula,

L = r × p

Where,

• r is Position Vector from Axis of Rotation
• p is Linear Momentum

Differentiating with respect to time, 

dL/dt = d/dt(r × p)

dL/dt = r × (dp/dt) + (dr/dt) × p…(i)

Now,

(dr/dt) = v and (dp/dt) = F

From eq(i)

dL/dt =  r × F + m(v × v)

Now, (v × v) = 0

∴ dL/dt = r × F

But, r × F = τ

∴ τ = dL/dt

Thus, if τ = 0, dL/dt = 0 or L = constant

As a result, in the absence of uneven external torque τ, angular momentum L is conserved. This is principle of angular momentum conservation, which is similar to linear momentum conservation.

What is Torque?

The force that may cause an object to rotate along an axis is measured by torque. In linear kinematics, force is what propels an object forward. An angular acceleration is also caused by torque. As a result, torque can be thought of as the linear force’s rotating equivalent. The axis of rotation is the point around which an object rotates. Torque is defined as a force’s proclivity to turn or twist in physics.

Formula of Torque is, 

τ = r × F

where, 

• r is Perpendicular Distance
• F is Force Applied of Object

Read More,

• Impulse
• Momentum
• Law Conservation of Momentum

Points to Remember

• Angular Momentum is defined as the attribute of any rotating object that is determined by the product of the moment of inertia and angular velocity.
• Magnitude of angular momentum ‘L’ can be calculated using the following formula: L = rmv sin Φ
• Spin and orbital angular momentum are the two types of angular momentum.
• L = r × p is the formula for calculating the angular momentum of a point object.
• L = I × ω is the formula for calculating the angular momentum of a long object.
• Radius of Circle determines a body’s perpendicular velocity when no torque is applied.

Angular Momentum-FAQs

1. What is Angular Momentum?

Angular momentum is defined as the product of Moment of Inertia and Angular Velocity of any Rotating Object.

2. What is Principle of Conservation of Angular Momentum?

According to the Law of Conservation of Angular momentum, when no external torque acting on the system, the angular momentum of the object is always conserved.

3. Is Angular Momentum is Scalar or Vector Quantity?

Angular Momentum has both magnitude and direction, therefore it is a Vector Quantity.

4. What is Angular Momentum Quantum Number?

Azimuthal quantum number or secondary quantum number is interchangeable with angular momentum quantum number. It is a quantum number that determines the angular momentum of an atomic orbital as well as its size and form. The most common value is between 0 and 1.

5. What is Angular Momentum and Moment of Inertia?

Angular Momentum of any object is the product of the Moment of Inertia and the Angualr Velocity of an object. Whereas, Moment of Inertia (MOI) is the measure of how the mass of object is distributed about the axis of rotation.

6. Is Angular Momentum Always Conserved?

No, Angular momentum is conserved only when no net external torque is applied to rotating body.