Angle between two Planes in 3D
Last Updated :
16 Sep, 2022
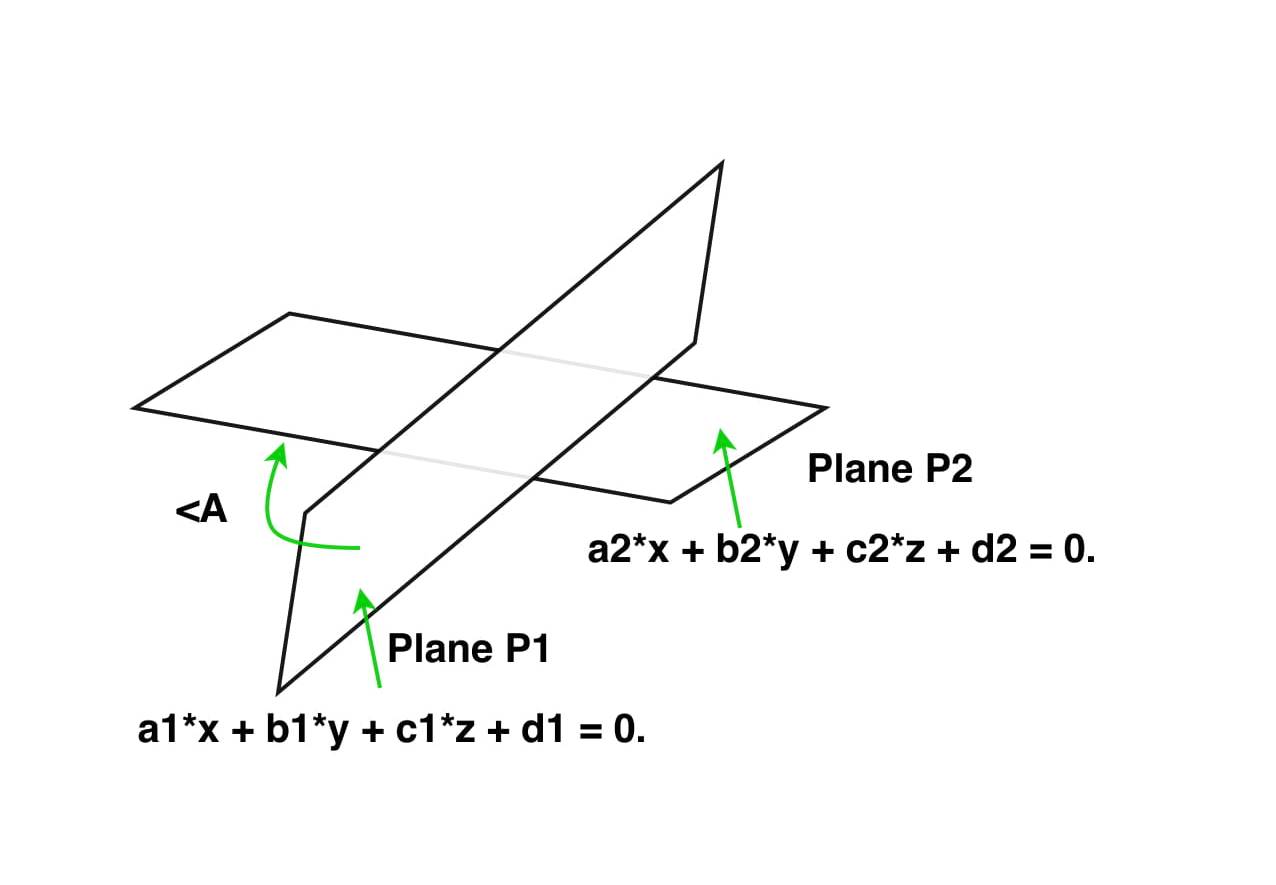
Given two planes P1: a1 * x + b1 * y + c1 * z + d1 = 0 and P2: a2 * x + b2 * y + c2 * z + d2 = 0. The task is to find the angle between these two planes in 3D.
Examples:
Input: a1 = 1, b1 = 1, c1 = 2, d1 = 1, a2 = 2, b2 = -1, c2 = 1, d2 = -4
Output: Angle is 60.0 degree
Input: a1 = 2, b1 = 2, c1 = -3, d1 = -5, a2 = 3, b2 = -3, c2 = 5, d2 = -6
Output: Angle is 123.696598882 degree
Approach: Consider the below equations of given two planes:
P1 : a1 * x + b1 * y + c1 * z + d1 = 0 and,
P2 : a2 * x + b2 * y + c2 * z + d2 = 0,
where a1, b1, c1, and a2, b2, c2 are direction ratios of normal to the plane P1 and P2.
The angle between two planes is equal to the angle determined by the normal vectors of the planes.
Angle between these planes is given by using the following formula:-
Cos A = 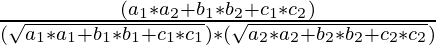
Using inverse property, we get:
A = 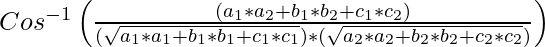
Below is the implementation of the above formulae:
C++
#include <bits/stdc++.h>
#include<math.h>
using namespace std;
void distance(float a1, float b1,
float c1, float a2,
float b2, float c2)
{
float d = (a1 * a2 + b1 *
b2 + c1 * c2);
float e1 = sqrt(a1 * a1 + b1 *
b1 + c1 * c1);
float e2 = sqrt(a2 * a2 + b2 *
b2 + c2 * c2);
d = d / (e1 * e2);
float pi = 3.14159;
float A = (180 / pi) * (acos(d));
cout << "Angle is "
<< A << " degree";
}
int main()
{
float a1 = 1;
float b1 = 1;
float c1 = 2;
float d1 = 1;
float a2 = 2;
float b2 = -1;
float c2 = 1;
float d2 = -4;
distance(a1, b1, c1,
a2, b2, c2);
return 0;
}
|
C
#include<stdio.h>
#include<math.h>
void distance(float a1, float b1,
float c1, float a2,
float b2, float c2)
{
float d = (a1 * a2 + b1 *
b2 + c1 * c2);
float e1 = sqrt(a1 * a1 + b1 *
b1 + c1 * c1);
float e2 = sqrt(a2 * a2 + b2 *
b2 + c2 * c2);
d = d / (e1 * e2);
float pi = 3.14159;
float A = (180 / pi) * (acos(d));
printf("Angle is %.2f degree", A);
}
int main()
{
float a1 = 1;
float b1 = 1;
float c1 = 2;
float d1 = 1;
float a2 = 2;
float b2 = -1;
float c2 = 1;
float d2 = -4;
distance(a1, b1, c1,
a2, b2, c2);
return 0;
}
|
Java
import java .io.*;
import java.lang.Math;
class GFG
{
static void distance(float a1, float b1,
float c1, float a2,
float b2, float c2)
{
float d = (a1 * a2 + b1 *
b2 + c1 * c2);
float e1 = (float)Math.sqrt(a1 * a1 + b1 *
b1 + c1 * c1);
float e2 = (float)Math.sqrt(a2 * a2 + b2 *
b2 + c2 * c2);
d = d / (e1 * e2);
float pi = (float)3.14159;
float A = (180 / pi) * (float)(Math.acos(d));
System.out.println("Angle is "+ A +" degree");
}
public static void main(String[] args)
{
float a1 = 1;
float b1 = 1;
float c1 = 2;
float d1 = 1;
float a2 = 2;
float b2 = -1;
float c2 = 1;
float d2 = -4;
distance(a1, b1, c1,
a2, b2, c2);
}
}
|
Python
import math
def distance(a1, b1, c1, a2, b2, c2):
d = ( a1 * a2 + b1 * b2 + c1 * c2 )
e1 = math.sqrt( a1 * a1 + b1 * b1 + c1 * c1)
e2 = math.sqrt( a2 * a2 + b2 * b2 + c2 * c2)
d = d / (e1 * e2)
A = math.degrees(math.acos(d))
print("Angle is"), A, ("degree")
a1 = 1
b1 = 1
c1 = 2
d1 = 1
a2 = 2
b2 = -1
c2 = 1
d2 = -4
distance(a1, b1, c1, a2, b2, c2)
|
C#
using System;
class GFG
{
static void distance(float a1, float b1,
float c1, float a2,
float b2, float c2)
{
float d = (a1 * a2 + b1 *
b2 + c1 * c2);
float e1 = (float)Math.Sqrt(a1 * a1 + b1 *
b1 + c1 * c1);
float e2 = (float)Math.Sqrt(a2 * a2 + b2 *
b2 + c2 * c2);
d = d / (e1 * e2);
float pi = (float)3.14159;
float A = (180 / pi) * (float)(Math.Acos(d));
Console.Write("Angle is "+ A +" degree");
}
public static void Main()
{
float a1 = 1;
float b1 = 1;
float c1 = 2;
float a2 = 2;
float b2 = -1;
float c2 = 1;
distance(a1, b1, c1,
a2, b2, c2);
}
}
|
PHP
<?php
function distance($a1, $b1,
$c1, $a2,
$b2, $c2)
{
$d = ($a1 * $a2 + $b1 *
$b2 + $c1 * $c2);
$e1 = sqrt($a1 * $a1 + $b1 *
$b1 + $c1 * $c1);
$e2 = sqrt($a2 * $a2 + $b2 *
$b2 + $c2 * $c2);
$d = $d / ($e1 * $e2);
$pi = 3.14159;
$A = (180 / $pi) * (acos($d));
echo sprintf("Angle is %.2f degree", $A);
}
$a1 = 1;
$b1 = 1;
$c1 = 2;
$d1 = 1;
$a2 = 2;
$b2 = -1;
$c2 = 1;
$d2 = -4;
distance($a1, $b1, $c1,
$a2, $b2, $c2);
?>
|
Javascript
<script>
function distance(a1, b1, c1, a2, b2, c2)
{
var d = a1 * a2 + b1 * b2 + c1 * c2;
var e1 = Math.sqrt(a1 * a1 + b1 * b1 + c1 * c1);
var e2 = Math.sqrt(a2 * a2 + b2 * b2 + c2 * c2);
d = parseFloat(d / (e1 * e2));
var pi = 3.14159;
var A = (180 / pi) * Math.acos(d);
document.write("Angle is " + A.toFixed(1) + " degree");
}
var a1 = 1;
var b1 = 1;
var c1 = 2;
var d1 = 1;
var a2 = 2;
var b2 = -1;
var c2 = 1;
var d2 = -4;
distance(a1, b1, c1, a2, b2, c2);
</script>
|
Output: Angle is 60.0 degree
Time complexity: O(logn) because using inbuilt sqrt function
Auxiliary function: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...