Angle between a Pair of Lines in 3D
Last Updated :
02 Feb, 2022
Given coordinates of three points A(x1, y1, z1), B(x2, y2, z2), and C(x3, y3, z3) in a 3D plane, where B is the intersection point of line AB and BC, the task is to find the angle between lines AB and BC.

Examples:
Input: x1 = 1, y1 = 3, z1 = 3; x2 = 3, y2 = 4, z2 = 5; x3 = 5, y3 = 6, z3 = 9;
Output: 54.6065
Input: x1 = 10, y1 = 10, z1 = 10; x2 = 0, y2 = 0, z2 = 0; x3 = 15, y3 = 10, z3 = 15;
Output: 56.4496
Approach:
1. Find the equation of lines AB and BC with the given coordinates in terms of direction ratios as:
AB = (x1 – x2)i + (y1 – y2)j + (z1 – z2)k
BC = (x3 – x2)i + (y3 – y2)j + (z3 – z2)k
2. Use the formula for cos ? for the two direction ratios of lines AB and BC to find the cosine of the angle between lines AB and BC as:
 where,
where,
AB.BC is the dot product of direction ratios AB and BC.
|AB| is the magnitude of line AB
|BC| is the magnitude of line BC
3. Suppose there are two direction ratios:
A = ai + bj + ck
B = xi + yj + zk
then
Dot Product(A.B) = a*x + b*y + c*z
magnitude of A = |A| = 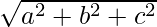
magnitude of B = |B| = 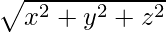
4. The cosine of the angle calculated gives the cosine value in radian. To find the angle multiply the cosine value by (180/?).
Below is the implementation of the above approach:
C++
#include "bits/stdc++.h"
#define PI 3.14
using namespace std;
void calculateAngle(
int x1, int y1, int z1,
int x2, int y2, int z2,
int x3, int y3, int z3)
{
int ABx = x1 - x2;
int ABy = y1 - y2;
int ABz = z1 - z2;
int BCx = x3 - x2;
int BCy = y3 - y2;
int BCz = z3 - z2;
double dotProduct
= ABx * BCx
+ ABy * BCy
+ ABz * BCz;
double magnitudeAB
= ABx * ABx
+ ABy * ABy
+ ABz * ABz;
double magnitudeBC
= BCx * BCx
+ BCy * BCy
+ BCz * BCz;
double angle = dotProduct;
angle /= sqrt(
magnitudeAB * magnitudeBC);
angle = (angle * 180) / PI;
cout << abs(angle) << endl;
}
int main()
{
int x1 = 1, y1 = 3, z1 = 3;
int x2 = 3, y2 = 4, z2 = 5;
int x3 = 5, y3 = 6, z3 = 9;
calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void calculateAngle(int x1, int y1, int z1,
int x2, int y2, int z2,
int x3, int y3, int z3)
{
int ABx = x1 - x2;
int ABy = y1 - y2;
int ABz = z1 - z2;
int BCx = x3 - x2;
int BCy = y3 - y2;
int BCz = z3 - z2;
double dotProduct = ABx * BCx +
ABy * BCy +
ABz * BCz;
double magnitudeAB = ABx * ABx +
ABy * ABy +
ABz * ABz;
double magnitudeBC = BCx * BCx +
BCy * BCy +
BCz * BCz;
double angle = dotProduct;
angle /= Math.sqrt(magnitudeAB * magnitudeBC);
angle = (angle * 180) / 3.14;
System.out.printf("%.4f", Math.abs(angle));
}
public static void main(String[] args)
{
int x1 = 1, y1 = 3, z1 = 3;
int x2 = 3, y2 = 4, z2 = 5;
int x3 = 5, y3 = 6, z3 = 9;
calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3);
}
}
|
Python3
import math
def calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3):
ABx = x1 - x2;
ABy = y1 - y2;
ABz = z1 - z2;
BCx = x3 - x2;
BCy = y3 - y2;
BCz = z3 - z2;
dotProduct = (ABx * BCx +
ABy * BCy +
ABz * BCz);
magnitudeAB = (ABx * ABx +
ABy * ABy +
ABz * ABz);
magnitudeBC = (BCx * BCx +
BCy * BCy +
BCz * BCz);
angle = dotProduct;
angle /= math.sqrt(magnitudeAB *
magnitudeBC);
angle = (angle * 180) / 3.14;
print(round(abs(angle), 4))
if __name__=='__main__':
x1, y1, z1 = 1, 3, 3;
x2, y2, z2 = 3, 4, 5;
x3, y3, z3 = 5, 6, 9;
calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3);
|
C#
using System;
class GFG{
static void calculateAngle(int x1, int y1,
int z1, int x2,
int y2, int z2,
int x3, int y3,
int z3)
{
int ABx = x1 - x2;
int ABy = y1 - y2;
int ABz = z1 - z2;
int BCx = x3 - x2;
int BCy = y3 - y2;
int BCz = z3 - z2;
double dotProduct = ABx * BCx +
ABy * BCy +
ABz * BCz;
double magnitudeAB = ABx * ABx +
ABy * ABy +
ABz * ABz;
double magnitudeBC = BCx * BCx +
BCy * BCy +
BCz * BCz;
double angle = dotProduct;
angle /= Math.Sqrt(magnitudeAB *
magnitudeBC);
angle = (angle * 180) / 3.14;
Console.Write(String.Format("{0:F4}", Math.Abs(angle)));
}
public static void Main()
{
int x1 = 1, y1 = 3, z1 = 3;
int x2 = 3, y2 = 4, z2 = 5;
int x3 = 5, y3 = 6, z3 = 9;
calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3);
}
}
|
Javascript
<script>
var PI = 3.14;
function calculateAngle(
x1, y1, z1,
x2, y2, z2,
x3, y3, z3)
{
var ABx = x1 - x2;
var ABy = y1 - y2;
var ABz = z1 - z2;
var BCx = x3 - x2;
var BCy = y3 - y2;
var BCz = z3 - z2;
var dotProduct
= ABx * BCx
+ ABy * BCy
+ ABz * BCz;
var magnitudeAB
= ABx * ABx
+ ABy * ABy
+ ABz * ABz;
var magnitudeBC
= BCx * BCx
+ BCy * BCy
+ BCz * BCz;
var angle = dotProduct;
angle /= Math.sqrt(
magnitudeAB * magnitudeBC);
angle = (angle * 180) / PI;
document.write(Math.abs(angle).toFixed(4));
}
var x1 = 1, y1 = 3, z1 = 3;
var x2 = 3, y2 = 4, z2 = 5;
var x3 = 5, y3 = 6, z3 = 9;
calculateAngle(x1, y1, z1,
x2, y2, z2,
x3, y3, z3);
</script>
|
Share your thoughts in the comments
Please Login to comment...