Analytical Approach to optimize Multi Level Cache Performance
Last Updated :
21 Jan, 2021
Prerequisite – Multilevel Cache Organization
The execution time of a program is the product of the total number of CPU cycles needed to execute a program. For a memory system with a single level of caching, the total cycle count is a function of the memory speed and the cache miss ratio.
m(C) = f(S, C, A, B)
m(C) = Cache miss ratio
C = Cache Size
A = Associativity
S = Number of sets
B = Block Size
The portion of a particular cache that is attributable to the instruction data’s main memory is NMM and can be expressed in the form of a linear first-order function.
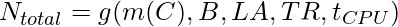
The most significant of these is the latency (LA), between the start of memory fetch and transferring of the requested data. The number of cycles spent waiting on main memory is denoted by LA, TR is the transfer rate which is the maximum rate at which data can be transferred also called the Baud rate.

As the above image illustrates the aforementioned linear relationship between the miss rate and the total cycle count. This makes it clear that as the organizational parameters increase in value the miss rate declines asymptomatically. This, in turn, causes the total cycle count to decline.
The most difficult relationship to quantify is between the cycle time of the CPU and the parameters that govern it because it depends on the lowest levels of implementations. An equation for it may look something like.
![Rendered by QuickLaTeX.com t_{CPU} = h(C,S,A,B)[3]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f50cef7674fe26744c77a8f54f7d23d2_l3.png)
Now the problem at hand becomes to relate system-level performance to the various cache and memory parameters.
Total execution time is a product of the cycle time and total cycle count.
![Rendered by QuickLaTeX.com T_{total} = t_{CPU}\times N_{total} = t_{L1}(C) \times N_{total} [4]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d94d119b6bdd4e0dd86c041ae8ad65f_l3.png)
To obtain the minimum execution time we find the partial derivative with respect to some variable is equal to zero.
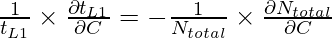
For non-continuous discrete variables, the above equation has a different form which is.
![Rendered by QuickLaTeX.com \frac{1}{ t_{L1}} \times \frac{\Delta t_{L1}}{\Delta C}=-\frac{1}{N_{total}}\times \frac{\Delta N_{total}}{\Delta C}[5]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b8076d3e7e2b0d096c63e9dbc68001a_l3.png)
If for one period then the change is performance neutral. But if the left-hand side is greater than the change increases overall execution time and if the right-hand side is more positive than there is a net gain in performance.
For a single level of caching, the total number of cycles is given by the number of cycles spent not performing memory references; plus the number of cycles spent doing instruction fetches, loads, and stores; plus the time spent waiting on main memory.
![Rendered by QuickLaTeX.com N_{total} = N_{Execute}+N_{Ifetch}\times m(C)\times \bar n_{MMread} +N_{load}+N_{Load}\times m(C)\times \bar n_{MMread} +N_{Store}\times \bar n_{L1write}[6]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c5a31fef3a24bde2a095de2841e494a_l3.png)
Nexecute = Number of cycles spent not performing a memory reference
NIfetch = Number of instruction fetches in the program or trace
NLoad = Number of loads
NStore = Number of Stores
nMMread = Average number of cycles spent satisfying a read cache miss
nL1write = Average number of cycles spent dealing with a write to the cache for RISC machines with single-cycle execution the number of cycles in which neither reference is active NExecute is zero.
We can now put all the operands of equation 6 which happen in parallel as 1 because they cumulatively take that much amount of time only. Then equation 6 becomes.
![Rendered by QuickLaTeX.com N_{total} = n_{Read}(1+m_{Read}(C)\times \bar n_{MMread})+N_{Store}\times \bar n_{L1write}[7]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0eda73a5992e94f7e20a815643bed332_l3.png)
For a machine with single-cycle execution and Harvard architecture capable of parallel instruction data and data reference generation loads contribute to the cycle count only if they miss in the data cache.
![Rendered by QuickLaTeX.com N_{Total} = N_{Ifetch} +N_{Ifetch}\times m(\textbf C_{L1t})\times \bar n_{MMread} +N_{Load}\times m(\textbf C_{L1D}\times \bar n_{MMread}) +N_{store}\times (n_{L1write}-1)[8]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8fa882567af14f48fcbcdd1d790e237f_l3.png)
Share your thoughts in the comments
Please Login to comment...