Ambiguous Grammar
Last Updated :
01 Aug, 2022
You can also read our previously discussed article on the Classification of Context-Free Grammar. Context Free Grammars(CFGs) are classified based on:
- Number of Derivation trees
- Number of strings
Depending on the Number of Derivation trees, CFGs are sub-divided into 2 types:
- Ambiguous grammars
- Unambiguous grammars
Ambiguous grammar: A CFG is said to be ambiguous if there exists more than one derivation tree for the given input string i.e., more than one LeftMost Derivation Tree (LMDT) or RightMost Derivation Tree (RMDT). Definition: G = (V,T,P,S) is a CFG that is said to be ambiguous if and only if there exists a string in T* that has more than one parse tree. where V is a finite set of variables. T is a finite set of terminals. P is a finite set of productions of the form, A -> ?, where A is a variable and ? ? (V ? T)* S is a designated variable called the start symbol.
For Example:
Let us consider this grammar: E -> E+E|id We can create a 2 parse tree from this grammar to obtain a string id+id+id. The following are the 2 parse trees generated by left-most derivation:
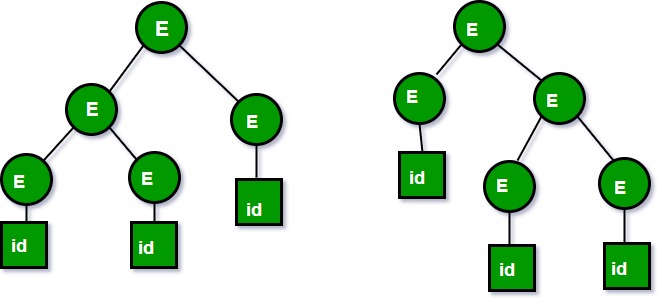
Both the above parse trees are derived from the same grammar rules but both parse trees are different. Hence the grammar is ambiguous. 2. Let us now consider the following grammar:
Set of alphabets ? = {0,…,9, +, *, (, )}
E -> I
E -> E + E
E -> E * E
E -> (E)
I -> ? | 0 | 1 | … | 9
From the above grammar String 3*2+5 can be derived in 2 ways:
I) First leftmost derivation II) Second leftmost derivation
E=>E*E E=>E+E
=>I*E =>E*E+E
=>3*E+E =>I*E+E
=>3*I+E =>3*E+E
=>3*2+E =>3*I+E
=>3*2+I =>3*2+I
=>3*2+5 =>3*2+5
Following are some examples of ambiguous grammar:
- S-> aS |Sa| ?
- E-> E +E | E*E| id
- A -> AA | (A) | a
- S -> SS|AB , A -> Aa|a , B -> Bb|b
Whereas following grammars are unambiguous:
- S -> (L) | a, L -> LS | S
- S -> AA , A -> aA , A -> b
Inherently ambiguous Language: Let L be a Context Free Language (CFL). If every Context-Free Grammar G with Language L = L(G) is ambiguous, then L is said to be inherently ambiguous Language. Ambiguity is a property of grammar not languages. Ambiguous grammar is unlikely to be useful for a programming language because two parse tree structures(or more) for the same string(program) imply two different meanings (executable programs) for the program. An inherently ambiguous language would be absolutely unsuitable as a programming language because we would not have any way of fixing a unique structure for all its programs. For example,
L = {anbncm} ? {anbmcm}
Note: Ambiguity of grammar is undecidable, i.e. there is no particular algorithm for removing the ambiguity of grammar, but we can remove ambiguity by Disambiguate the grammar i.e., rewriting the grammar such that there is only one derivation or parse tree possible for a string of the language which the grammar represents. This article is compiled by Saikiran Goud Burra.
Some Questions on ambiguous grammar
1) How to find out whether grammar is ambiguous or not?
Ans:- if we can directly or indirectly observe both left and right recursion in grammar, then the grammar is ambiguous.
Example - S -> SaS|?
In this grammar we can see both left and right recurtion. So the grammar is ambiguous.
We can make more than one parse tree/derivation tree for input string (let's say {aa} )

Parse Tree
2) If both left and right recursion are not present in grammar, then is the grammar unambiguous? Explain with an example.
Ans– No, the grammar can still be ambiguous. If both left and right recursion are present in grammar, then the grammar is ambiguous, but the reverse is not always true.
Example -
S -> aB | ab
A -> AB | a
B -> Abb | b
In the above example, although both left and right recursion are not present, but if we see string { ab }, we can make more than one parse tree to generate the string.

Parse Tree
From the above example, we can see that even if both left and right recursion are not present in grammar, the grammar can be ambiguous.
3) State whether the grammar is ambiguous or not.
S -> SAB | ?
A -> AaB | a
B -> AS | b
Ans – The grammar is Ambiguous.
If we put
B -> AS in S -> SAB
Then we get S -> SAAS and the grammar clearly contains both left and right recursion. Hence the grammar is ambiguous.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...