Algorithms Sample Questions | Set 3 | Time Order Analysis
Last Updated :
28 May, 2019
Question 1: What is the asymptotic boundary of T(n)?
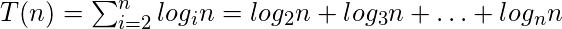
- θ( n*log(n) )
- θ( n2 )
- θ( n )
- θ( n*log2(n) )
- θ( n2*log2(n) )
Answer: 3
Explanation: To find appropriate upper and lower boundaries, an approach which first comes to mind is to expand the sigma notation to single terms among which some patterns can be detected. This way it helps to define some acceptable upper and lower boundaries and their combination might lead to a possible solution.
Regarding specifying these boundaries, there are some hints as following:
-
This is obvious that for any k greater than √ n, each logkn should be less than log√nn = 2, while more than lognn = 1. In mathematic language:
- A hint on UPPER boundary, for k > √ n:
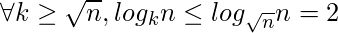
![Rendered by QuickLaTeX.com \Rightarrow \sum_{i=[\sqrt{n}]}^{ n } log_{i}n \leq \sum_{i=[\sqrt{n}]}^{ n } 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db9f1a658d930759424b4e0329e14891_l3.png)
- A hint on LOWER boundary, for k > √ n:

![Rendered by QuickLaTeX.com \Rightarrow \sum_{i=[\sqrt{n}] + 1}^{ n } log_{i}n \geq \sum_{i=[\sqrt{n}] + 1}^{ n } 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bda39c60c18aab07aa6739252aa2198a_l3.png)
-
Besides that, as the base of a logarithm increases, its value decreases; so none of the terms resulted from expansion of the first sigma can be more than the first ter, log2n, nor can be less than the last one, which is log√nn; in other sentences,
- Another hint on UPPER boundary, but this time for k < √ n:

![Rendered by QuickLaTeX.com \Rightarrow \sum_{i=2}^{ [\sqrt{n}] } log_{i}n \leq \sum_{i=2}^{ [\sqrt{n}] } log_{2}n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ccf61475ec5ce05ff753fc1a4f5b8993_l3.png)
- Another hint on LOWER boundary, but this time for k < √ n:
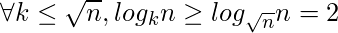
![Rendered by QuickLaTeX.com \Rightarrow \sum_{i=2}^{ [\sqrt{n}] } log_{i}n \geq \sum_{i=2}^{ [\sqrt{n}] } 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc28fd0fe008667f793f768624f3e76c_l3.png)
Following these hints gives:
- Lower boundary:
![Rendered by QuickLaTeX.com \sum_{i=2}^{n} log_{i}n = \sum_{i=2}^{ [\sqrt{n}] } log_{i}n + \sum_{i=[\sqrt{n}]+1}^{n} log_{i}n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31b086e28e32bbb571998b9d8ef06528_l3.png)
![Rendered by QuickLaTeX.com \leq \sum_{i=2}^{ [\sqrt{n}] } log_{2}n + \sum_{i=[\sqrt{n}]+1}^{n} 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed1572dcf8dffb1f2b064db4a97762df_l3.png)
![Rendered by QuickLaTeX.com = ([\sqrt{n}] - 1) * log_{2}n + (n - [\sqrt{n}]) * 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa23e976f2a244af05a46c958fc6f306_l3.png)
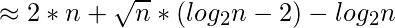
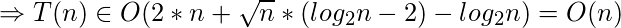
- Upper boundary:
![Rendered by QuickLaTeX.com \sum_{i=2}^{n} log_{i}n = \sum_{i=2}^{ [\sqrt{n}] } log_{i}n + \sum_{i=[\sqrt{n}]+1}^{n} log_{i}n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31b086e28e32bbb571998b9d8ef06528_l3.png)
![Rendered by QuickLaTeX.com \geq \sum_{i=2}^{ [\sqrt{n}] } log_{[\sqrt{n}]}n + \sum_{i=[\sqrt{n}]+1}^{n} 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-811322822a7bad2abe8508096b023e3b_l3.png)
![Rendered by QuickLaTeX.com = ([\sqrt{n}] - 1) * 2 + (n - [\sqrt{n}]) * 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6534bc6204e40bad33f6e22e295e779_l3.png)
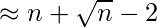
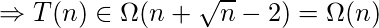
What has been derived till now indicates that the growth of T(n) cannot exceed O(n), nor can be less than Ω(n); Therefore, the asymptotic complexity order of T(n) is:
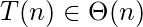
Question 2: What is running time order of given program?
C PROGRAM: Input n of type integer
for(i= 2; i<n; i=i+1)
for(j = 1; j < n; j= j * i)
// A line of code of Θ(1)
- θ( n )
- θ( n*log(n) )
- θ( n2 )
- θ( n*log2log(n) )
- θ( n2*log2(n) )
Answer: 1
Explanation: The running time of each line is indicated below separately:
- The first code line, t1(n), is:
for(i= 2; i<n; i=i+1) // it runs (n – 2) times; so the time complexity of this line is of θ(n)
- The second code line, t2(n) is:
for(j = 1; j < n; j= j * i) // log2n + log3n + … + logn-1n = Σlogin ∈ Θ( n ) in according to PREVIOUS QUESTION of this article (Refer to Question 1)
- The third code line, t3(n) is:
//A code line of Θ(1) :: Inside loops, so its order time is as the same as that of previous line, which is of Θ( n )
The total time complexity T(n) of the program is the sum of each line t
i(n), i = 1..3, as following:
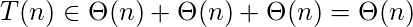
Question 3: The following recurrence equation T(n) is given. How many number of proposed g
i(n), i=1 .. 5, functions is acceptable in order to have T(n) ∈ θ(f(n)) when f(n) = g
i(n)?
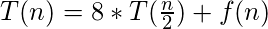
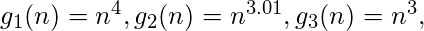
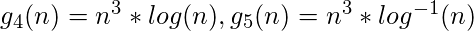
- 1
- 2
- 3
- 4
- 5
Answer: 2
Explanation: Master theorem and its extension can be of great help to easily tackle this problem. The general form of
master theorem can be expressed as:
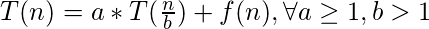
In order to use the
master theorem, there is a need to see that the given problem with specific “a”, “b”, and “f(n)” satisfies the condition of which case of this theorem. The three cases of
master theorem and their conditions are:
-
case 1: This case happens the recursion tree is leaf-heavy (the work to split/recombine a problem is dwarfed by subproblems.)

-
case 2: This case occurs when the work to split/recombine a problem is comparable to subproblems.
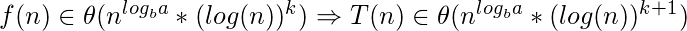
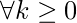
-
case 3: This case takes place when the recursion tree is root-heavy (the work to split/recombine a problem dominates subproblems.)
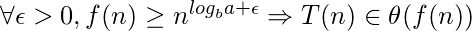
The generalized second case of master theorem, so-called
advanced master theorem, handles all values of k. It says:
The answer to this question is the third case of master theorem where T(n) is of Θ( f(n) ); so in order to have T(n) = θ(f(n)), there should be polynomial difference “epsilon” between n
logba and f(n); therefore, the functions g
1(n) and g
2(n) meet the conditions of third case of Master theorem. The value of “epsilon” found for them are 1 and 0.01 respectively.
Question 4: Which option delineates a true asymptotic analysis for this multiple input variable program, while having an insight (prior knowledge) about the relative growth of inputs, like m ∈ Θ(n)?
C PROGRAM: inputs m and n of type integer
for(i= 1; i<= n; i=i+1) : n
for(j = 1; j <= m; j= j * 2)
for(k = 1; k <= j; k= k+1)
\\ A code line of Θ(1)
- θ( n * m*(m+1)/2 )
- θ( n*m + n*log2(m) )
- θ( m3 )
- θ( n2 )
- θ( n2*log2(n) )
Answer: 4
Explanation: To compute the time complexity of program based on inputs n and m, T(n, m), the first step is to obtain the running time of each line, t
i(n, m), as indicated below:
-
for(i= 1; i<= n; i=i+1) // It runs n times
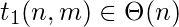
-
for(j = 1; j <= m; j= j * 2) // iterates log2(m) times, and it is inside another loop which multiply it n times
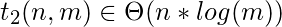
-
for(k = 1; k <= j; k= k+1) // It runs 2 + 4 + 8 + … + 2log(m) times
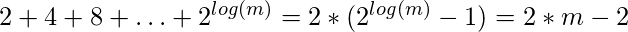
This is also inside an outer loop, first “for” loop, which itself iterates n times
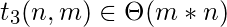
-
\\A line of code of Θ(1) The same as previous line, Θ( m*n )
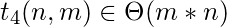
The total running time order of this program is:
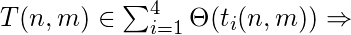
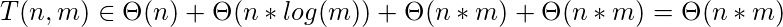
It can even be more simplified in according to the given prior knowledge which says that m ∈ Θ(n), or n ∈ Θ(m):
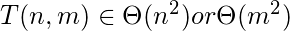
Question 5: There is a vector of integer numbers, called V[], which is of length “N”.
For a specific problem (program), it is given that Σ
i=1N |V[i]| = P.
What is the time complexity of following code snippet? [Needless to say, P is also an integer number]
Tmp = -1;
For r= 1 to N
For S = 1 to V[r]
Tmp = Tmp + 20;
- O( N + 2*N*P )
- O( N * P )
- O( N2 )
- O( P2 )
- O( 2*P + N )
Answer: 5
Explanation: The number of time each line will be executed and their total time complexity is indicated below:
Tmp = -1; // θ(1)
For r= 1 to N // N times; so it is of θ(N)
For S = 1 to V[r] // Cannot be more than |V[r]| times; so the total number of times is O(Σ
r=1N |V[r]| ) = O(P)
Tmp = Tmp + 20; // The same as previous line, O( P )
In order to find the time complexity of the given program, there are three facts to keep on mind:
- Each V[r] can take any integer value (even zero or negative ones), but it doesn’t matter as all negative values will lead to no execution of the second loop in programming languages like C. However, in programming languages, it is allowed to count down-to (or to iterate over) negative numbers, but the algorithms are not being analyzed depends on programming languages, and the analysis is just based on the algorithm itself. What to say for sure is the information that is given in the question; so a shrewd action is to consider the absolute value of |V[r]| and also to use O() notation in order to get rid of being stuck. Otherwise, it has to be said that the program runs at least as much as the time needed for just execution of the first loop, or Ω(N)
- Although the running time order of this program does not seem to depend on two variables, but there is no more information for further analysis which is needed to compare P and N; so the asymptotic complexity depends on the values of both P and N; in other words, there is T(N, P) complexity function instead of T(N).
- The O() notation defines a looser boundary than the tight boundary specified by &theta() notation; Therefore, the sum of θ() and O() would be of O() type. In this problem, the total time complexity of the program, which is the sum of all code lines complexities, θ(1) + θ(N) + O( P ) + O( P ), belongs to set O( 2 * P + N + 1 ) or O(2*P + N).
Considering all factors mentioned above, one asymptotic complexity can be of
T(N, P) ∈ O(2*|P| + N); However, the coefficients of variables are not important at the final step of asymptotic analysis, as they all belong to the same set of complexity functions, and the complexity can also be expressed as O(|P| + N).
Source:
-
A compilation of Iran university exams (with a bit of summarization, modification, and also translation)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...