Top MCQs on Graph Traversals with Answers
Question 1
Which of the following algorithms can be used to most efficiently determine the presence of a cycle in a given graph ?
Question 3
What are the appropriate data structures for following algorithms?
1) Breadth-First Search
2) Depth First Search
3) Prim\'s Minimum Spanning Tree
4) Kruskal\' Minimum Spanning Tree
Question 4
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
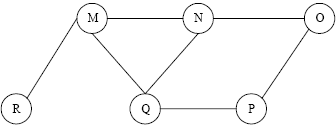 [/caption]
[/caption]Question 5
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true? (GATE CS 2000)
Question 6
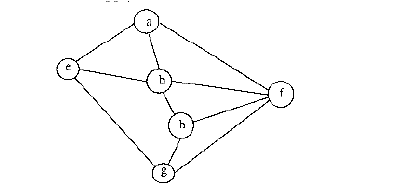
Among the following sequences:
(I) a b e g h f (II) a b f e h g (III) a b f h g e (IV) a f g h b eWhich are depth first traversals of the above graph?
Question 7
Which of the following condition is sufficient to detect cycle in a directed graph?
Question 8
Is following statement true/false If a DFS of a directed graph contains a back edge, any other DFS of the same graph will also contain at least one back edge.
Question 9
Make is a utility that automatically builds executable programs and libraries from source code by reading files called makefiles which specify how to derive the target program. Which of the following standard graph algorithms is used by Make.
Question 10
Given two vertices in a graph s and t, which of the two traversals (BFS and DFS) can be used to find if there is path from s to t?
There are 30 questions to complete.