Algebra of Real Functions

A function can be thought of as a rule or set of rules which map an input to an output knows as its image. 

x ⇢ Function ⇢ y

Letters such as f, g, or h are often used to describe function. Sometimes while working on complex problems, combining two or more functions is required. Suppose, we have a function that computes cubes of the numbers given as input but we want that the output should always be a positive number. In this case, one might need to combine a cube function with an absolute function. Such combinations are often employed in real life, but it cannot be done as easily every time as it was in this case. We need to take care of things so that combinations do not give undefined output. Let’s look at the rules or algebra of the functions which help us in combining them. 

Algebra of real functions

Addition of Functions

Let f:X → R and g:X → R be any two real functions, where X ∈ R. Then we define (f + g):X → R by 

(f + g) (x) = f (x) + g (x), for all x ∈ X

Let D(f) and D(g) be the domain of function “f” and “g” respectively. The domain in the case of function addition becomes. 

D(f + g) = D(f) ∩ D(g)

Question: Given f(x) = x + 3 and g(x) = 2x. Find (f + g)(x). 

Solution:

(f + g) (x) = f (x) + g (x). Since f(x) = x + 3 and g(x) = 2x. 

(f + g)(x) = x + 3 + 2x = 3x + 3

Since domain for both the functions is real number R. The intersection of domain is also R. So, domain of (f + g)(x) is R. 

Subtraction of Functions

Let f:X → R and g:X → R be any two real functions, where X ∈ R. Then we define (f – g):X → R by

(f – g) (x) = f (x) – g (x), for all x ∈ X

Let D(f) and D(g) be the domain of function “f” and “g” respectively. The domain in the case of function addition becomes.

D(f + g) = D(f) ∩ D(g)

Question: Given f(x) = x² + 1 and g(x) = 1/x. Find (f-g)(x). 

Solution:

Domain for f(x) is R but domain for g(x) is R – {0}.  

(f – g)(x) = f(x) – g(x)  = x² + 1 – 1/x. But the domain for (f – g)(x) is R ∩ R – {0} = R – {0}. 

Multiplication by a Scalar

Let f: X → R be a real function and “k” be any scalar belonging to R. Then the product kf is a function from X to R defined by 

(kf)(x) = kf(x), x ∈ X.

The domain remains the same in this case. 

Multiplication of two real functions

Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then product of these two functions i.e. f ∗ g : X → R is defined by

 (f ∗ g) (x) = f (x) g (x) ∀ x ∈ X

Let D(f) and D(g) be the domain of function “f” and “g” respectively. In this case also the domain 

D(f * g) = D(f) ∩ D(g)

Question: Given f(x) = x² + 1 and g(x) = 1/x. Find (f ∗ g)(x). 

Solution:

(f * g)(x) = f(x) g(x) = (x2 + 1)(1/x) = 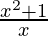. Domain remains the same as previous example in this case too. 

Quotient of two real function

Let f and g be two real functions defined from X → R. The quotient of f by g is denoted by 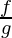 is a function defined from X → R as, 

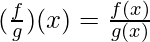, provided g(x) ≠ 0.

The domain for 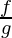: {x | x ∈ D_f ∩ D_g and g(x) ≠ 0}

Question 1: Given f(x) = x² + 1 and g(x) = (x + 1)/x. Find 

Solution:

Domain for f(x) is R and Domain for g(x) is R – {0}. Also, g(x) = 0 at x  = -1. 

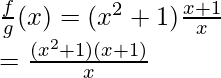
We know, domain should be  {x | x ∈ Df ∩ Dg and g(x) ≠ 0 }. 

So, domain becomes R – {0,1}. 

Question 2: Given the tables below: 

x	2	4	6	8
f(x)	23	16	30	26

x	2	4	6	8
g(x)	28	32	-14	-22

Calculate: 

• (f + g)(6)
• (f – g)(8)
• (f * g)(2)
• (f/g)(4)

Answer: 

• (f + g)(6) = f (6) + g(6) = 30 + (-14) = 16
• (f – g)(8) = f (8) – g(8) = 26 – (-22) = 48
• (f * g)(2) = f (2) x g(2) = 23 x 28 = 644
• (f / g)(4) = f (4) / g(4) = 16 / 32 = ½