Algebra of Derivative of Functions
Last Updated :
26 Feb, 2024
Derivatives are an integral part of calculus. They measure the rate of change in any quantity. Suppose there is a water tank from which water is leaking. A local engineer is asked to measure the time in which the water tank will become empty. In such a scenario, the engineer needs to know two things — the size of the water tank and the rate at which water is flowing out of it. The size of the tank can be found out easily but to measure the rate at which water is leaking he will have to use derivatives. In this way, derivatives are intertwined in our lives. It is easy to calculate the derivatives for simple functions, but when functions become complex the correct way to approach this problem is to break the problem into subproblems that are easier to solve. Let’s see some rules and approaches to do that in the case of derivatives.
What is Derivatives?
Derivatives are built on top of the concept of limits. They measure the difference between the values of a function in an interval whose width approaches the value zero. For example, let’s say a function f(x) is given and the goal is to calculate the derivative of that function at a point x = a using limits. It is denoted by 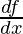 , or f'(x).
, or f'(x).
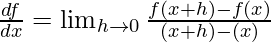
At x = a,
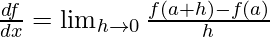

Notice in the figure, as the interval “h” approaches zero. The line approaches to being a tangent from a chord. This means, that now the derivative when h approaches zero, gives us the slope of the tangent at that particular point.
Derivatives of some Basic Functions
The table below shows the derivatives of some standard basic functions.
| Common Function | Function | Derivative |
| Constant Function | c | f'(x) = 0 |
| Line | Ax + b | f'(x) = A |
| Square | x2 | f'(x) = 2x |
| Square Root | √x | f'(x) = 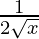 |
| Exponential | ex | ex |
| Exponential | ax | ln(a).ax |
| Logarithms | logex | 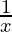 |
| Logarithms | logax | 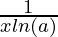 |
| Trigonometry | sin(x) | cos(x) |
| Trigonometry | cos(x) | -sin(x) |
| Trigonometry | tan(x) | sec2(x) |
Rules of Differentiation
The above table presents us derivatives of some standard functions, but in real life, the functions are not always simple. Usually, the functions encountered involve more than one function related to each other by the operators such as addition, subtraction, multiplication, and division. In such cases, it is very cumbersome to solve the derivatives through their limits definition. To make such calculations easy certain rules were given:
- Summation or Difference Rule
- Product and Division Rule
Consider two functions f(x) and g(x). Let’s say there is a third function h(x) which combines these two functions.
Summation and Difference Rule
Case 1: h(x) = f(x) + g(x)
This function is summation of both f(x) and g(x), the derivative of such functions is given by,
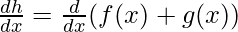
⇒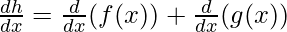
or
h'(x) = f'(x) + g'(x)
Case 2: h(x) = f(x) – g(x)
This function is the difference of both f(x) and g(x), the derivative of such functions is given by,
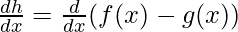
⇒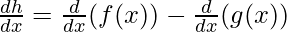
or
h'(x) = f'(x) – g'(x)
Product and Division Rules
Case (i): h(x) = f(x) x g(x)
This function is product of both f(x) and g(x), the derivative of such functions is given by,
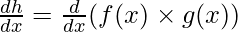
⇒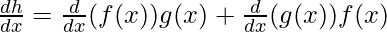
or
h'(x) = f'(x)g(x) + g'(x) f(x)
Case (i): h(x) = 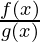
This function is division of both f(x) and g(x), the derivative of such functions is given by,
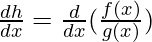
⇒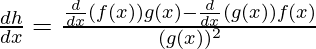
or
h'(x) = 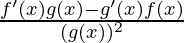
The division and product rules are also called the Leibniz rules.
Let’s see some sample problems with these rules.
Problems on Algebra of Derivative
Problem 1: Find the derivative for the given function f(x).
f(x) = x2 + 3x
Solution:
This function is the sum of two different function. Sum rule will be used here.
f(x) = x2 + 3x
Here, h(x) = x2 and g(x) = 3x.
f(x) = h(x) + g(x)
⇒f'(x) = h'(x) + g'(x)
⇒ f'(x) = 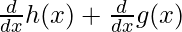
⇒f'(x) =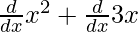
⇒f'(x) = 2x + 3
Problem 2: Find the derivative for the given function f(x).
f(x) = ex + sin(x)
Solution:
This function is the sum of two different function. Sum rule will be used here.
f(x) = ex + sin(x)
Here, h(x) =ex and g(x) = sin(x)
f(x) = h(x) + g(x)
⇒f'(x) = h'(x) + g'(x)
⇒ f'(x) = 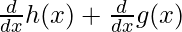
⇒f'(x) =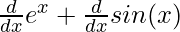
⇒f'(x) = ex + cos(x)
Problem 3: Find the derivative for the given function f(x),
f(x) = 5x4 – 3x2
Solution:
This function is the difference of two different function. Difference rule will be used here.
f(x) = 5x4 – 3x2
Here, h(x) =5x4 and g(x) = 3x2
f(x) = h(x) – g(x)
⇒f'(x) = h'(x) – g'(x)
⇒ f'(x) = 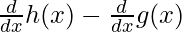
⇒f'(x) =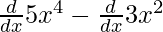
⇒f'(x) = 20x3 – 6x
Problem 4: Find the derivative for the given function f(x),
f(x) = 5log(x) – 3x
Solution:
This function is the difference of two different function. Difference rule will be used here.
f(x) = 5log(x) – 3x
Here, h(x) =5log(x) and g(x) = 3x
f(x) = h(x) – g(x)
⇒f'(x) = h'(x) – g'(x)
⇒ f'(x) = 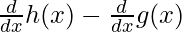
⇒f'(x) =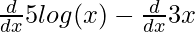
⇒f'(x) = 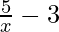
Problem 5: Find the derivative for the given function f(x),
f(x) = 5x4.sin(x)
Solution:
This function is the product of two different function. Product rule will be used here.
f(x) = 5x4.sin(x)
Here, h(x) =5x4 and g(x) = sin(x)
f(x) = h(x).g(x)
⇒f'(x) = h'(x) g(x) + h(x)g'(x)
⇒ f'(x) = 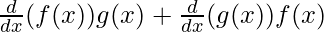
⇒f'(x) =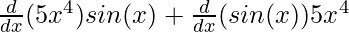
⇒f'(x) = 20x3sin(x) + 5x4cos(x)
Problem 6: Find the derivative for the given function f(x),
f(x) = 5ex.log(x)
Solution:
This function is the product of two different function. Product rule will be used here.
f(x) = 5ex.log(x)
Here, h(x) =5ex and g(x) = log(x)
f(x) = h(x).g(x)
⇒f'(x) = h'(x) g(x) + h(x)g'(x)
⇒ f'(x) = 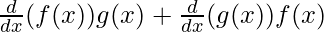
⇒f'(x) =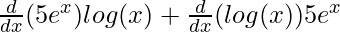
⇒f'(x) = 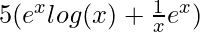
Problem 7: Find the derivative for the given function f(x),
f(x) = 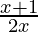
Solution:
This function is the division of two different function. Division rule will be used here.
f(x) =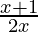
Here, h(x) =x + 1 and g(x) = 2x
f(x) = 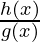
⇒f'(x) = 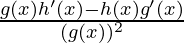
⇒ f'(x) = 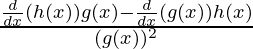
⇒f'(x) =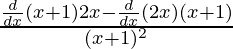
⇒f'(x) =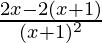
⇒f'(x) = 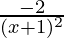
Problem 8: Find the derivative for the given function f(x),
f(x) = 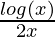
Solution:
This function is the division of two different function. Division rule will be used here.
f(x) =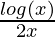
Here, h(x) =log(x) and g(x) = 2x
f(x) = 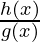
⇒f'(x) = 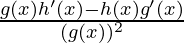
⇒ f'(x) = 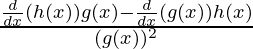
⇒f'(x) =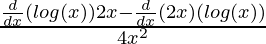
⇒f'(x) =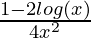
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...