Algebra
Question 1
Given two numbers x and y such that
1. x3 + y3 = 9
2. x + y = 3
Find the value of x4+y4
Question 3
If x takes only real numbers. For what value of x, the value of the expression: 4−6x−x2 will be maximum?
Question 9
4/15 of 5/7 of a number is greater than 4/9 of 2/5 of the same number by 8. What is half of that number?
There are 20 questions to complete.
Last Updated :
Take a part in the ongoing discussion

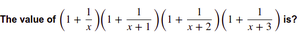 [/caption]
[/caption]