Activation functions in Neural Networks
Last Updated :
17 Feb, 2023
It is recommended to understand Neural Networks before reading this article.
In the process of building a neural network, one of the choices you get to make is what Activation Function to use in the hidden layer as well as at the output layer of the network. This article discusses some of the choices.
Elements of a Neural Network
Input Layer: This layer accepts input features. It provides information from the outside world to the network, no computation is performed at this layer, nodes here just pass on the information(features) to the hidden layer.
Hidden Layer: Nodes of this layer are not exposed to the outer world, they are part of the abstraction provided by any neural network. The hidden layer performs all sorts of computation on the features entered through the input layer and transfers the result to the output layer.
Output Layer: This layer bring up the information learned by the network to the outer world.
What is an activation function and why use them?
The activation function decides whether a neuron should be activated or not by calculating the weighted sum and further adding bias to it. The purpose of the activation function is to introduce non-linearity into the output of a neuron.
Explanation: We know, the neural network has neurons that work in correspondence with weight, bias, and their respective activation function. In a neural network, we would update the weights and biases of the neurons on the basis of the error at the output. This process is known as back-propagation. Activation functions make the back-propagation possible since the gradients are supplied along with the error to update the weights and biases.
Why do we need Non-linear activation function?
A neural network without an activation function is essentially just a linear regression model. The activation function does the non-linear transformation to the input making it capable to learn and perform more complex tasks.
Mathematical proof
Suppose we have a Neural net like this :-
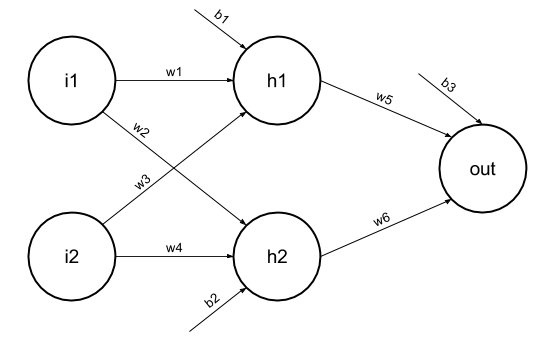
Elements of the diagram are as follows:
Hidden layer i.e. layer 1:
z(1) = W(1)X + b(1) a(1)
Here,
- z(1) is the vectorized output of layer 1
- W(1) be the vectorized weights assigned to neurons of hidden layer i.e. w1, w2, w3 and w4
- X be the vectorized input features i.e. i1 and i2
- b is the vectorized bias assigned to neurons in hidden layer i.e. b1 and b2
- a(1) is the vectorized form of any linear function.
(Note: We are not considering activation function here)
Layer 2 i.e. output layer :-
Note : Input for layer 2 is output from layer 1
z(2) = W(2)a(1) + b(2)
a(2) = z(2)
Calculation at Output layer
z(2) = (W(2) * [W(1)X + b(1)]) + b(2)
z(2) = [W(2) * W(1)] * X + [W(2)*b(1) + b(2)]
Let,
[W(2) * W(1)] = W
[W(2)*b(1) + b(2)] = b
Final output : z(2) = W*X + b
which is again a linear function
This observation results again in a linear function even after applying a hidden layer, hence we can conclude that, doesn’t matter how many hidden layer we attach in neural net, all layers will behave same way because the composition of two linear function is a linear function itself. Neuron can not learn with just a linear function attached to it. A non-linear activation function will let it learn as per the difference w.r.t error. Hence we need an activation function.
Variants of Activation Function
Linear Function
- Equation : Linear function has the equation similar to as of a straight line i.e. y = x
- No matter how many layers we have, if all are linear in nature, the final activation function of last layer is nothing but just a linear function of the input of first layer.
- Range : -inf to +inf
- Uses : Linear activation function is used at just one place i.e. output layer.
- Issues : If we will differentiate linear function to bring non-linearity, result will no more depend on input “x” and function will become constant, it won’t introduce any ground-breaking behavior to our algorithm.
For example : Calculation of price of a house is a regression problem. House price may have any big/small value, so we can apply linear activation at output layer. Even in this case neural net must have any non-linear function at hidden layers.
Sigmoid Function
- It is a function which is plotted as ‘S’ shaped graph.
- Equation : A = 1/(1 + e-x)
- Nature : Non-linear. Notice that X values lies between -2 to 2, Y values are very steep. This means, small changes in x would also bring about large changes in the value of Y.
- Value Range : 0 to 1
- Uses : Usually used in output layer of a binary classification, where result is either 0 or 1, as value for sigmoid function lies between 0 and 1 only so, result can be predicted easily to be 1 if value is greater than 0.5 and 0 otherwise.
Tanh Function
- The activation that works almost always better than sigmoid function is Tanh function also known as Tangent Hyperbolic function. It’s actually mathematically shifted version of the sigmoid function. Both are similar and can be derived from each other.
- Equation :-
- Value Range :- -1 to +1
- Nature :- non-linear
- Uses :- Usually used in hidden layers of a neural network as it’s values lies between -1 to 1 hence the mean for the hidden layer comes out be 0 or very close to it, hence helps in centering the data by bringing mean close to 0. This makes learning for the next layer much easier.
RELU Function
- It Stands for Rectified linear unit. It is the most widely used activation function. Chiefly implemented in hidden layers of Neural network.
- Equation :- A(x) = max(0,x). It gives an output x if x is positive and 0 otherwise.
- Value Range :- [0, inf)
- Nature :- non-linear, which means we can easily backpropagate the errors and have multiple layers of neurons being activated by the ReLU function.
- Uses :- ReLu is less computationally expensive than tanh and sigmoid because it involves simpler mathematical operations. At a time only a few neurons are activated making the network sparse making it efficient and easy for computation.
In simple words, RELU learns much faster than sigmoid and Tanh function.
Softmax Function
The softmax function is also a type of sigmoid function but is handy when we are trying to handle multi- class classification problems.
- Nature :- non-linear
- Uses :- Usually used when trying to handle multiple classes. the softmax function was commonly found in the output layer of image classification problems.The softmax function would squeeze the outputs for each class between 0 and 1 and would also divide by the sum of the outputs.
- Output:- The softmax function is ideally used in the output layer of the classifier where we are actually trying to attain the probabilities to define the class of each input.
- The basic rule of thumb is if you really don’t know what activation function to use, then simply use RELU as it is a general activation function in hidden layers and is used in most cases these days.
- If your output is for binary classification then, sigmoid function is very natural choice for output layer.
- If your output is for multi-class classification then, Softmax is very useful to predict the probabilities of each classes.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...