Acceleration due to Gravity

Acceleration due to gravity (or acceleration of gravity) or gravity acceleration is the acceleration caused by the gravitational force of attraction of large bodies. As we know that the term acceleration is defined as the rate of change of velocity with respect to a given time. Scientists like Sir Isaac Newton and Lord Henry Cavendish soon discovered that this increase in speed, or acceleration, was caused by a different force known as gravity by studying objects falling to the Earth in a variety of circumstances. According to definitions, gravity is a force that pulls objects toward the center of mass, like the Earth. Conversely, acceleration describes how an object’s velocity or speed changes over time. Hence, the value of acceleration due to gravity is 9.8 m/s² on earth.

What is Acceleration due to Gravity?

Acceleration due to Gravity is defined as the acceleration attained by an object due to the gravitational force of attraction. When a body is fallen toward the earth it experiences a change in its acceleration due to the gravitational pull (or force) of the Earth. This acceleration is called acceleration due to gravity. This is the acceleration that is attained by an object due to gravitational force. 

The acceleration that an object experiences as a result of the gravitational force is known as acceleration due to gravity, ms^-2 is its SI unit. It has a direction and a magnitude so it is a vector quantity as a result.

The symbol g represents the acceleration due by gravity. Its typical value at sea level on the surface of the earth is 9.8 ms^-2. The second law of motion and the law of universal gravitation of Newton serve as the foundation for its calculation.

Acceleration due to Gravity Formula

Mathematically, the acceleration due to gravity is directly proportional to the mass of the object and inversely proportional to the distance from the center of mass, so given as:

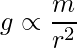
or

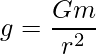
where, 

• g is the acceleration due to gravity,
• G is the Gravitational constant, 
• m is the mass of the body and 
• r is the distance from the center.

Units of Acceleration due to Gravity

• The SI unit of Acceleration due to Gravity is m/s².
• The CGS unit of g is cm/s².
• And the dimensional formula of Acceleration due to Gravity is [ML⁰T^-2].

Derivation for the formula of acceleration due to gravity

According to the second law of motion:

F = ma

But, in case of a free-falling body, the force is equal to the product of the mass of the body and acceleration due to gravity.

F = mg        ……(1)

But, according to the universal law of gravitation:

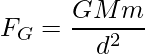      ……(2)

Now, from the equation (1) and (2),

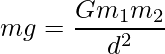
Consider for an ideal case the object is placed near to earth therefore the distance between earth and object will be radius of earth, so replace d with r and rearranging the above expression for g as:

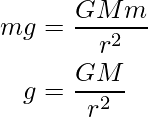
Calculation of the Value of Acceleration due to Gravity 

The acceleration due to gravity is stated as:

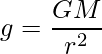
Here, substitute 6.67 × 10^-11 Nm² kg^-2 for G, 6 × 10²⁴ kg for M and 6.4 × 10⁶ m for r in the above expression to calculate g at the surface of Earth.

Hence, the value of acceleration due to gravity on the surface of Earth is 9.8 m/s².

Factor affecting Acceleration due to Gravity

• Shape of Earth: It is known that the shape of the earth is not spherical it’s quite oval so the gravitational force is different at different places. The force of attraction is maximum at the pole of the earth approximately 9.82 m/s² as the radius of the earth is minimum at the pole. While the force of gravitation is minimum at the equator of the earth at approximately 9.78 m/s² as the radius of the earth is maximum at the equator
• Altitude: When a body moves away from the surface of the earth the force of attraction decreases as the distance between the earth and the body increases.
• Depth: When a body is put inside the earth’s surface the acceleration due to gravity becomes less.

Effects on g due to Height (h)

Consider an object (of mass m) P at a height h from the surface of the earth, R be the radius of the earth as shown in the figure below:

The gravitational force F acting on the mass m is,

F = GMm/ (R+h)²

where, M is the mass of the Earth.

Since, F = mg_h, where g_h is the acceleration due to gravity at height h. Then the above equation becomes:

mg_h = GMm/(R+h)²

g_h = GM/r² (1+h/r)²

= (GM/r²)/(1+h/r)²

Since, g = GM/r²

Therefore, 

g_h = g / (1+h/r)²

Now, if h is much lesser than the radius of the earth, the value of g at height h is given by:

g_h = g/(1 – 2h/r)

Effects on g due to Depth D

Consider an object (of mass m) P at a depth d from the surface of the earth, R be the radius of the earth as shown in the figure below:

The acceleration due to gravity at the surface of Earth in terms of density is:

g = 4/3 x  πρ x RG

At depth D,

g_D = 4/3 x  πρ x (R-D)G

On dividing both equations we get,

g_d = g x πρ x (R-D)

Now two cases can be possible:

Case 1: If depth D is equal to the radius of the earth i.e. D = R, then:

g_d = 0

Case 2: If depth D = 0, i.e. the object is at the surface of earth, then

g_d = g

Effects on g due to Shape of Earth 

The radius of the earth, an oblate spheroid, is greater towards the equator than it is farther from the poles. The acceleration caused by gravity changes with latitude due to the shape of the earth since it is inversely proportional to the square of the earth’s radius for a given mass.

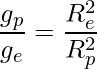
where, 

• R_e and R_p are the radii of Earth at the equator and the poles, and 
• g_e and g_p are the acceleration due to gravity at the equator and poles, respectively.

Hence, from the above-mentioned equation, it is obvious that the equator experiences less, and the poles have more gravitational acceleration. Therefore, when g lowers, a person’s weight falls as they move from the equator to the poles.

Effects on g due to the Rotation

The variation in g is due to the centrifugal force acting on the rotation of the earth. When the earth is rotating, all the objects tend to experience a centrifugal force that won’t act in the direction of gravity.

FAQs on Acceleration due to Gravity

Question 1: What do you mean by Acceleration due to Gravity?

Answer:

Acceleration due to Gravity is defined as the acceleration attained by an object due to the gravitational force of attraction. When a body is fallen toward the earth it experiences a change in its acceleration due to the gravitational pull (or force) of the Earth. 

Question 2: What is the SI unit and dimensional formula of Acceleration due to Gravity?

Answer:

The SI unit of Acceleration due to Gravity is m/s². And the dimensional formula of Acceleration due to Gravity is [ML⁰T^-2].

Question 3: What is the acceleration due to gravity on the moon?

Answer:

The value of acceleration due to gravity on the moon is 1.625 m/s².

Question 4: Does the mass of any object have an impact on the value of acceleration due to gravity?

Answer:

No, mass does not have any significant impact on the value of acceleration due to gravity.

Question 5: Write down the formula to calculate the attraction force between two objects.

Answer:

The formula to calculate the attraction force between two objects is given by,

F = GMm/ R²

where, 

• m and M are the masses of the objects in contact, 
• G is the Gravitational Constant and 
• R is the distance between them.

Question 6: What do you understand by the term Free Fall?

Answer:

A body is said to be in free fall when it only moves with respect to the Earth’s gravity. An external force exerted on the ball will cause its motion to accelerate. Gravitational acceleration is another name for this rate of free fall.