Abstraction of Binary Search
Last Updated :
26 May, 2021
What is the binary search algorithm?
Binary Search Algorithm is used to find a certain value of x for which a certain defined function f(x) needs to be maximized or minimized. It is frequently used to search an element in a sorted sequence by repeatedly dividing the search interval into halves. Begin with an interval covering the whole sequence, if the value of the search key is less than the item in the middle of the interval, then search in the left half of the interval otherwise search in the right half. Repeatedly check until the value is found or the interval is empty.
The main condition to perform a Binary Search is that the sequence must be monotonous i.e., it must be either increasing or decreasing.
Monotonic function
A function f(x) is said to be monotonic if and only if for any x if f(x) returns true, then for any value of y (where y > x) should also return true and similarly if for a certain value of x for which f(x) is false, then for any value z (z < x) the function should also return false.
How to solve a question using Binary Search:
If the function is
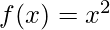
And the task is to find the maximum value of x such that f(x) is less than or equal to the target value. The interval in which we will search the target value for the given
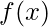
is from 0 to target value.
Then we can use binary search for this problem since the function
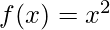
is a monotonically increasing function.
Target = 17
f(x) = x2, since the function is monotonic binary search can be applied to it.
Range of search interval will be [0, target]
Step 1:
low = 0, high = 17, calculate mid = (low + high)/2 = 8
Calculate f(8) = 64 which is more than target, so it will return false and high will be updated as high = mid – 1 = 7.
Steps 2:
low = 0, high = 7, calculate mid = (low + high)/2 = 3
Calculate f(3) = 9 which is less than target, so it will return true and low will be updated as low = mid + 1 = 4.
Step 3:
low = 4, high = 7, calculate mid = (low + high)/2 = 5
Calculate f(5) = 25 which is more than target, so it will return false and high will be updated as high = mid – 1 = 4.
Step 4:
Now since the range [low, high] converges to a single point i.e 4 so the final result is found, since f(4) = 16 which is the maximum value of the given function less than target.
Below is the implementation of the above example:
C++
#include "bits/stdc++.h"
using namespace std;
void findX(int targetValue)
{
int start = 0, end = targetValue;
int mid, result;
while (start <= end) {
mid = start + (end - start) / 2;
if (mid * mid <= targetValue) {
result = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
cout << result << endl;
}
int main()
{
int targetValue = 81;
findX(targetValue);
}
|
Java
import java.util.*;
class GFG{
static void findX(int targetValue)
{
int start = 0, end = targetValue;
int mid = 0, result = 0;
while (start <= end)
{
mid = start + (end - start) / 2;
if (mid * mid <= targetValue)
{
result = mid;
start = mid + 1;
}
else
{
end = mid - 1;
}
}
System.out.print(result + "\n");
}
public static void main(String[] args)
{
int targetValue = 81;
findX(targetValue);
}
}
|
Python3
def findX(targetValue):
start = 0;
end = targetValue;
mid = 0;
while (start <= end):
mid = start + (end - start) // 2;
if (mid * mid <= targetValue):
result = mid
start = mid + 1;
else:
end = mid - 1;
print(result);
if __name__ == '__main__':
targetValue = 81;
findX(targetValue);
|
C#
using System;
class GFG{
static void findX(int targetValue)
{
int start = 0, end = targetValue;
int mid = 0, result = 0;
while (start <= end)
{
mid = start + (end - start) / 2;
if (mid * mid <= targetValue)
{
result = mid;
start = mid + 1;
}
else
{
end = mid - 1;
}
}
Console.Write(result + "\n");
}
public static void Main(String[] args)
{
int targetValue = 81;
findX(targetValue);
}
}
|
Javascript
<script>
function findX(targetValue)
{
var start = 0, end = targetValue;
var mid, result;
while (start <= end) {
mid = start + parseInt((end - start) / 2);
if (mid * mid <= targetValue) {
result = mid;
start = mid + 1;
}
else {
end = mid - 1;
}
}
document.write( result );
}
var targetValue = 81;
findX(targetValue);
</script>
|
The above binary search algorithm requires at most O(log N) comparisons to find the maximum value less than or equal to the target value. And the value of the function f(x) = x2 doesn’t need to be evaluated many times.
Time Complexity: O(logN)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...