Optimal Substructure Property in Dynamic Programming | DP-2
Last Updated :
27 Mar, 2023
As we discussed in Set 1, the following are the two main properties of a problem that suggest that the given problem can be solved using Dynamic programming:
1) Overlapping Subproblems
2) Optimal Substructure
We have already discussed the Overlapping Subproblem property in Set 1. Let us discuss the Optimal Substructure property here.
In Dynamic programming, the ideal base property alludes to the way that an ideal answer for an issue can be built from ideal answers for subproblems. This property is utilized to plan dynamic programming calculations that tackle streamlining issues by separating them into more modest subproblems and afterward consolidating the answers for those subproblems to get an answer for the first issue.
For instance, think about the issue of tracking down the most brief way between two focuses in a diagram.
On the off chance that we apply dynamic programming to this issue, we can characterize the subproblems as the briefest ways between halfway focuses on the chart, and afterward utilize the answers for those subproblems to build an answer for the first issue.
To show this thought all the more officially, we should assume we disapprove of an ideal arrangement S* and a bunch of subproblems S1, S2, …, Sn. On the off chance that the ideal answer for the issue can be developed from the ideal answers for the subproblems, then the issue displays the ideal base property.
2) Optimal Substructure:
A given problem is said to have Optimal Substructure Property if the optimal solution of the given problem can be obtained by using the optimal solution to its subproblems instead of trying every possible way to solve the subproblems.
Example:
The Shortest Path problem has the following optimal substructure property:
If node x lies in the shortest path from a source node U to destination node V then the shortest path from U to V is a combination of the shortest path from U to X and the shortest path from X to V. The standard All Pair Shortest Path algorithm like Floyd–Warshall and Single Source Shortest path algorithm for negative weight edges like Bellman–Ford are typical examples of Dynamic Programming.
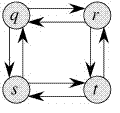
On the other hand, the Longest Path problem doesn’t have the Optimal Substructure property. Here by Longest Path, we mean the longest simple path (path without cycle) between two nodes. Consider the following unweighted graph given in the CLRS book. There are two longest paths from q to t: q?r?t and q?s?t. Unlike shortest paths, these longest paths do not have the optimal substructure property. For example, The longest path q?r?t is not a combination of the longest path from q to r and the longest path from r to t, because the longest path from q to r is q?s?t?r and the longest path from r to t is r?q?s?t.
Some Standard problems having optimal substructure are:
The above problems can be solved optimally using Dynamic programming as each of these problems have an optimal substructure, On the other hand, there are some problems that need to be solved by trying all possible solutions one such problem is Rat in a Maze problem. In these types of problems, the optimal solution for subproblems may not surely give the solution to the entire problem. In Rat in a Maze problem, all paths need to be explored to find out the final path from the source that leads to the destination. Thus in these problems, Recursion and Backtracking are the way to go.
Pseudo code:
for x in V:
for y in V:
dp[x][y] = INF
dp[u][u] = 0
for x in V:
for y in V:
for z in V:
if (x, y) is an edge in E:
dp[x][y] = min(dp[x][y], dp[x][z] + dp[z][y])
return dp[u][v]
C++
#include <iostream>
#include <algorithm>
#include <limits>
using namespace std;
const int N = 100010;
int n;
int adj[N][N];
int dist[N][N];
void floyd() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = adj[i][j];
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> adj[i][j];
if (adj[i][j] == 0) {
adj[i][j] = numeric_limits<int>::max();
}
}
}
floyd();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << i << " " << j << " " << dist[i][j] << endl;
}
}
return 0;
}
|
Java
import java.util.Arrays;
import java.util.List;
import java.util.Map;
class ShortestPath {
static final int INF = Integer.MAX_VALUE;
static int shortestPath(int[][] graph, int u, int v) {
int n = graph.length;
int[][] dp = new int[n][n];
for (int[] row : dp) {
Arrays.fill(row, INF);
}
dp[u][u] = 0;
for (int x = 0; x < n; x++) {
for (int y = 0; y < n; y++) {
for (int z = 0; z < n; z++) {
if (graph[x][y] != INF) {
dp[x][y] = Math.min(dp[x][y], dp[x][z] + dp[z][y]);
}
}
}
}
return dp[u][v];
}
public static void main(String[] args) {
int[][] graph = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
int shortestPath = shortestPath(graph, 0, 3);
System.out.println("Shortest path from 0 to 3: " + shortestPath);
}
}
|
Python3
N = 100010
adj = [[0 for j in range(N)] for i in range(N)]
dist = [[0 for j in range(N)] for i in range(N)]
def floyd():
global N, adj, dist
for i in range(N):
for j in range(N):
dist[i][j] = adj[i][j]
for k in range(N):
for i in range(N):
for j in range(N):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
if __name__ == "__main__":
n = int(input())
for i in range(n):
line = input().strip().split()
for j in range(n):
adj[i][j] = int(line[j])
if adj[i][j] == 0:
adj[i][j] = sys.maxsize
floyd()
for i in range(n):
for j in range(n):
print(i, j, dist[i][j])
|
C#
using System;
using System.Collections.Generic;
class ShortestPath {
static readonly int INF = int.MaxValue;
static int shortestPath(int[,] graph, int u, int v) {
int n = graph.GetLength(0);
int[,] dp = new int[n, n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i, j] = INF;
}
}
dp[u, u] = 0;
for (int x = 0; x < n; x++) {
for (int y = 0; y < n; y++) {
for (int z = 0; z < n; z++) {
if (graph[x, y] != INF) {
dp[x, y] = Math.Min(dp[x, y], dp[x, z] + dp[z, y]);
}
}
}
}
return dp[u, v];
}
public static void Main(string[] args) {
int[,] graph = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
int shortestpath = shortestPath(graph, 0, 3);
Console.WriteLine("Shortest path from 0 to 3: " + shortestpath);
}
}
|
Javascript
const Arrays = require('java.util.Arrays');
const List = require('java.util.List');
const Map = require('java.util.Map');
class ShortestPath {
static const INF = Number.MAX_VALUE;
static shortestPath(graph, u, v) {
const n = graph.length;
const dp = new Array(n).fill().map(() => new Array(n).fill(INF));
dp[u][u] = 0;
for (let x = 0; x < n; x++) {
for (let y = 0; y < n; y++) {
for (let z = 0; z < n; z++) {
if (graph[x][y] !== INF) {
dp[x][y] = Math.min(dp[x][y], dp[x][z] + dp[z][y]);
}
}
}
}
return dp[u][v];
}
static main(args) {
const graph = [
[0, 5, INF, 10],
[INF, 0, 3, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0]
];
const shortestPath = ShortestPath.shortestPath(graph, 0, 3);
console.log(`Shortest path from 0 to 3: ${shortestPath}`);
}
}
ShortestPath.main();
|
We will be covering some example problems in future posts on Dynamic Programming.
References:
http://en.wikipedia.org/wiki/Optimal_substructure
CLRS book
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...