2D Transformation in Computer Graphics | Set 1 (Scaling of Objects)
Last Updated :
22 Mar, 2023
We can use a 2 × 2 matrix to change or transform, a 2D vector. This kind of operation, which takes in a 2-vector and produces another 2-vector by a simple matrix multiplication, is a linear transformation.
By this simple formula, we can achieve a variety of useful transformations, depending on what we put in the entries of the matrix. For our purposes, consider moving along the x-axis a horizontal move and along the y-axis, a vertical move.
A scaling transformation alters size of an object. In the scaling process, we either compress or expand the dimension of the object. Scaling operation can be achieved by multiplying each vertex coordinate (x, y) of the polygon by scaling factor sx and sy to produce the transformed coordinates as (x’, y’). So, x’ = x * sx and y’ = y * sy. The scaling factor sx, sy scales the object in X and Y direction respectively. So, the above equation can be represented in matrix form: 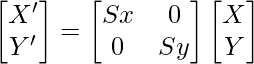 Or P’ = S . P Scaling process:
Or P’ = S . P Scaling process: 
Note: If the scaling factor S is less than 1, then we reduce the size of the object. If the scaling factor S is greater than 1, then we increase size of the object. Algorithm:
1. Make a 2x2 scaling matrix S as:
Sx 0
0 Sy
2. For each point of the polygon.
(i) Make a 2x1 matrix P, where P[0][0] equals
to x coordinate of the point and P[1][0]
equals to y coordinate of the point.
(ii) Multiply scaling matrix S with point
matrix P to get the new coordinate.
3. Draw the polygon using new coordinates.
Below is C implementation:
C
#include <conio.h>
#include <graphics.h>
#include <iostream>
#include <math.h>
#include <stdio.h>
int gd = DETECT, gm;
int n, x[100], y[100], i;
float sfx, sfy;
void draw();
void scale();
using namespace std;
int main()
{
cout << "Enter no. of sides in polygon: ";
cin >> n;
cout << "Enter coordinates x, y for each vertex: ";
for (i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
cout << "Enter scale factors: sfx and sfy : ";
cin >> sfx >> sfy;
initgraph(&gd, &gm, (char*)"");
cleardevice();
setcolor(RED);
draw();
scale();
setcolor(YELLOW);
draw();
getch();
closegraph();
return 0;
}
void draw()
{
for (i = 0; i < n; i++) {
line(x[i], y[i], x[(i + 1) % n], y[(i + 1) % n]);
}
}
void scale()
{
for (i = 0; i < n; i++) {
x[i] = x[0] + (int)((float)(x[i] - x[0]) * sfx);
y[i] = y[0] + (int)((float)(y[i] - y[0]) * sfx);
}
}
|
Output:
For Shearing
C
#include<stdio.h>
#include<graphics.h>
#include<conio.h>
#include<iostream>
#include<math.h>
int gd= DETECT, gm;
int n,x[100],y[100],i;
float sfx, sfy;
void draw();
void scale();
using namespace std;
int main(){
cout<<"Enter no. of sides in polygon: ";
cin>>n;
cout<<"Enter coordinates x, y for each vertex: ";
for(i=0;i<n;i++){
cin>>x[i]>>y[i];}
cout<<"Enter scale factors: sfx and sfy : ";
cin>>sfx>>sfy;
initgraph(&gd, &gm, (char*)"");
cleardevice();
setcolor(RED);
draw();
scale();
setcolor(YELLOW);
draw();
getch();
closegraph();
return 0;
}
void draw(){
for(i=0; i<n; i++){
line(x[i],y[i],x[(i+1)%n],y[(i+1)%n]);}
}
void scale(){
for(i=0; i<n; i++){
x[i]=x[0]+(int)((float)(x[i]-x[0])*sfx);
y[i]=y[0]+(int)((float)(y[i]-y[0])*sfx);
}
}
|
Output:
Code For Rotation
C
#include<stdio.h>
#include<graphics.h>
#include<math.h>
#include<iostream>
using namespace std;
int main()
{
int gd=0,gm,x1,y1,x2,y2,x3,y3;
double s,c, angle;
initgraph(&gd, &gm, (char*)"");
setcolor(RED);
cout<<"Enter coordinates of triangle: ";
cin>>x1>>y1;
cin>>x2>>y2;
cin>>x3>>y3;
setbkcolor(WHITE);
cleardevice();
line(x1,y1,x2,y2);
line(x2,y2, x3,y3);
line(x3, y3, x1, y1);
cout<<"Enter rotation angle: ";
cin>>angle;
c = cos(angle *M_PI/180);
s = sin(angle *M_PI/180);
x1 = floor(x1 * c + y1 * s);
y1 = floor(-x1 * s + y1 * c);
x2 = floor(x2 * c + y2 * s);
y2 = floor(-x2 * s + y2 * c);
x3 = floor(x3 * c + y3 * s);
y3 = floor(-x3 * s + y3 * c);
setcolor(GREEN);
line(x1, y1 ,x2, y2);
line(x2,y2, x3,y3);
line(x3, y3, x1, y1);
getch();
closegraph();
return 0;
}
|
Output:
Translation
C
#include <conio.h>
#include <graphics.h>
#include <iostream>
#include <stdio.h>
int gd = DETECT, gm;
int n, xs[100], ys[100], i, ty, tx;
void draw();
void translate();
using namespace std;
int main()
{
cout << "Enter no. of sides in polygon: ";
cin >> n;
cout << "Enter coordinates x, y for each vertex: ";
for (i = 0; i < n; i++) {
cin >> xs[i] >> ys[i];
}
cout << "Enter distances for translation (in x and y "
"directions): ";
cin >> tx >> ty;
initgraph(&gd, &gm, (char*)"");
cleardevice();
setcolor(RED);
draw();
translate();
setcolor(YELLOW);
draw();
getch();
closegraph();
return 0;
}
void draw()
{
for (i = 0; i < n; i++) {
line(xs[i], ys[i], xs[(i + 1) % n],
ys[(i + 1) % n]);
}
}
void translate()
{
for (i = 0; i < n; i++) {
xs[i] += tx;
ys[i] += ty;
}
}
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...