Write an Efficient Method to Check if a Number is Multiple of 3
Last Updated :
20 Mar, 2023
The very first solution that comes to our mind is the one that we learned in school. If the sum of digits in a number is a multiple of 3 then the number is a multiple of 3, e.g., for 612, the sum of digits is 9 so it’s a multiple of 3. But this solution is not efficient. You have to get all decimal digits one by one, add them and then check if the sum is a multiple of 3.
There is a pattern in the binary representation of a number that can be used to find if a number is a multiple of 3. If the difference between the count of odd set bits (Bits set at odd positions) and even set bits is a multiple of 3 then is the number.
Example: 23 (00..10111)
1) Get count of all set bits at odd positions (For 23 it’s 3).
2) Get count of all set bits at even positions (For 23 it’s 1).
3) If the difference between the above two counts is a multiple of 3 then the number is also a multiple of 3.
(For 23 it’s 2 so 23, is not a multiple of 3)
Take some more examples like 21, 15, etc…
Algorithm: isMutlipleOf3(n)
1) Make n positive if n is negative.
2) If number is 0 then return 1
3) If number is 1 then return 0
4) Initialize: odd_count = 0, even_count = 0
5) Loop while n != 0
a) If rightmost bit is set then increment odd count.
b) Right-shift n by 1 bit
c) If rightmost bit is set then increment even count.
d) Right-shift n by 1 bit
6) return isMutlipleOf3(odd_count - even_count)
Proof:
Let the binary representation of the number be: abcde.
In decimal form this number will be: 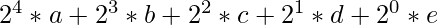
Every even power of 2 can be represented as 3n + 1, and every odd power of 2 can be represented as 3n – 1. For example:
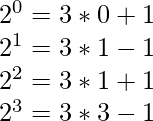 ans so on...
ans so on...
Therefore, the decimal form becomes:
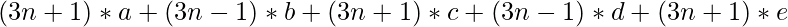 [Tex](3n)(a+b+c+d+e) + (a - b + c - d + e) \\[/Tex](multiple of 3)
[Tex](3n)(a+b+c+d+e) + (a - b + c - d + e) \\[/Tex](multiple of 3)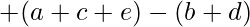
To have this number divisible by 3, the term 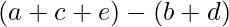 should be divisible by 3.
should be divisible by 3.
Therefore for the number to be divisible by, the difference between the count of odd set bits (a + c + e) and even set bits (b + d) should be divisible by 3.
Program:
C++
#include <bits/stdc++.h>
using namespace std;
int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
while (n) {
if (n & 1)
odd_count++;
if (n & 2)
even_count++;
n = n >> 2;
}
return isMultipleOf3(abs(odd_count - even_count));
}
int main()
{
int num = 24;
if (isMultipleOf3(num))
printf("%d is multiple of 3", num);
else
printf("%d is not a multiple of 3", num);
return 0;
}
|
Java
import java.lang.*;
import java.util.*;
class GFG {
static int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
while (n != 0) {
if ((n & 1) != 0)
odd_count++;
if ((n & 2) != 0)
even_count++;
n = n >> 2;
}
return isMultipleOf3(Math.abs(odd_count - even_count));
}
public static void main(String[] args)
{
int num = 24;
if (isMultipleOf3(num) != 0)
System.out.println(num + " is multiple of 3");
else
System.out.println(num + " is not a multiple of 3");
}
}
|
Python3
def isMultipleOf3(n):
odd_count = 0
even_count = 0
if(n < 0):
n = -n
if(n == 0):
return 1
if(n == 1):
return 0
while(n):
if(n & 1):
odd_count += 1
if(n & 2):
even_count += 1
n = n >> 2
return isMultipleOf3(abs(odd_count - even_count))
num = 24
if (isMultipleOf3(num)):
print(num, 'is multiple of 3')
else:
print(num, 'is not a multiple of 3')
|
C#
using System;
class GFG {
static int isMultipleOf3(int n)
{
int odd_count = 0, even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
while (n != 0) {
if ((n & 1) != 0)
odd_count++;
if ((n & 2) != 0)
even_count++;
n = n >> 2;
}
return isMultipleOf3(Math.Abs(odd_count - even_count));
}
public static void Main()
{
int num = 24;
if (isMultipleOf3(num) != 0)
Console.Write(num + " is multiple of 3");
else
Console.Write(num + " is not a multiple of 3");
}
}
|
PHP
<?php
function isMultipleOf3( $n)
{
$odd_count = 0;
$even_count = 0;
if($n < 0) $n = -$n;
if($n == 0) return 1;
if($n == 1) return 0;
while($n)
{
if($n & 1)
$odd_count++;
if($n & 2)
$even_count++;
$n = $n >> 2;
}
return isMultipleOf3(abs($odd_count -
$even_count));
}
$num = 24;
if (isMultipleOf3($num))
echo $num, "is multiple of 3";
else
echo $num, "is not a multiple of 3";
?>
|
Javascript
<script>
function isMultipleof3(n)
{
odd_count = 0;
even_count = 0;
if(n < 0)
n = -n;
if(n == 0)
return 1;
if(n == 1)
return 0;
while (n)
{
if(n & 1)
odd_count++;
if(n & 2)
even_count++;
n = n>>2;
}
return isMultipleof3(Math.abs(odd_count-even_count));
}
num = 24;
if(isMultipleof3(num))
document.write(num + " is multiple of 3");
else
document.write(num + " is not a multiple of 3");
</script>
|
Output24 is multiple of 3
Time Complexity: O(logn)
Auxiliary Space: O(1)
Efficient Method:
Use Dynamic Programming (Top-Down Approach Using Memoization)
C++
#include <bits/stdc++.h>
using namespace std;
int static dp[1001];
int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
if(dp[n] != -1)
return dp[n];
while (n) {
if (n & 1)
odd_count++;
if (n & 2)
even_count++;
n = n >> 2;
}
dp[n] = isMultipleOf3(abs(odd_count - even_count));
return dp[n];
}
int main()
{
int num = 24;
memset(dp, -1, sizeof(dp));
if (isMultipleOf3(num))
printf("%d is multiple of 3", num);
else
printf("%d is not a multiple of 3", num);
return 0;
}
|
C
#include <stdio.h>
#include<string.h>
int static dp[1001];
int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
if(dp[n] != -1)
return dp[n];
while (n) {
if (n & 1)
odd_count++;
if (n & 2)
even_count++;
n = n >> 2;
}
int abs = (odd_count - even_count);
if(abs<0)
{
abs= -1*abs;
}
dp[n] = isMultipleOf3(abs);
return dp[n];
}
int main()
{
int num = 24;
memset(dp, -1, sizeof(dp));
if (isMultipleOf3(num))
printf("%d is multiple of 3", num);
else
printf("%d is not a multiple of 3", num);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int []dp ;
static int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
if(dp[n] != -1)
return dp[n];
while (n > 0) {
if ((n & 1) != 0)
odd_count++;
if ((n & 2) != 0)
even_count++;
n = n >> 2;
}
dp[n] = isMultipleOf3(Math.abs(odd_count - even_count));
return dp[n];
}
public static void main(String[] args)
{
int num = 24;
dp = new int[1001];
Arrays.fill(dp, -1);
if (isMultipleOf3(num) == 1)
System.out.printf("%d is multiple of 3", num);
else
System.out.printf("%d is not a multiple of 3", num);
}
}
|
Python3
dp = [-1 for i in range(1001)];
def isMultipleOf3(n):
odd_count = 0;
even_count = 0;
if (n < 0):
n = -n;
if (n == 0):
return 1;
if (n == 1):
return 0;
if (dp[n] != -1):
return dp[n];
while (n > 0):
if ((n & 1) != 0):
odd_count+=1;
if ((n & 2) != 0):
even_count+=1;
n = n >> 2;
dp[n] = isMultipleOf3(abs(odd_count - even_count));
return dp[n];
if __name__ == '__main__':
num = 24;
if (isMultipleOf3(num) == 1):
print(num,"is multiple of 3");
else:
print(num," is not a multiple of 3");
|
C#
using System;
class GFG {
static int []dp = new int[1001];
static int isMultipleOf3(int n)
{
int odd_count = 0;
int even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
if(dp[n] != -1)
return dp[n];
while (n > 0) {
if ((n & 1) != 0)
odd_count++;
if ((n & 2) != 0)
even_count++;
n = n >> 2;
}
dp[n] = isMultipleOf3(Math.Abs(odd_count - even_count));
return dp[n];
}
public static void Main()
{
int num = 24;
for(int i = 0; i < 1001; i++) {
dp[i] = -1;
}
if (isMultipleOf3(num) == 1)
Console.Write(num + " is multiple of 3");
else
Console.Write(num + " is not a multiple of 3");
}
}
|
Javascript
<script>
let dp = [];
for(let i = 0; i < 1001; i++) {
dp[i] = -1;
}
function isMultipleOf3(n)
{
let odd_count = 0;
let even_count = 0;
if (n < 0)
n = -n;
if (n == 0)
return 1;
if (n == 1)
return 0;
if(dp[n] != -1)
return dp[n];
while (n) {
if (n & 1)
odd_count++;
if (n & 2)
even_count++;
n = n >> 2;
}
dp[n] = isMultipleOf3(Math.abs(odd_count - even_count));
return dp[n];
}
let num = 24;
if (isMultipleOf3(num))
document.write(num + " is multiple of 3");
else
document.write(num + " is not a multiple of 3");
</script>
|
Output24 is multiple of 3
Time Complexity: O(nlogn)
Auxiliary Space: O(n)
Method: Checking given number is multiple of 3 or not using modulo division.
C++
#include <iostream>
using namespace std;
int main()
{
int num = 24;
cout << num;
if (num % 3 == 0) {
cout << " is multiple of 3";
}
else {
cout << " is not multiple of 3";
}
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
public static void main(String[] args)
{
int num = 24;
System.out.println(num);
if ((n) % 3 == 0)
{
System.out.println(" is multiple of 3");
}
else
{
System.out.println(" is not multiple of 3");
}
}
}
|
Python3
num = 24
print(num,end="")
if (num % 3 is 0):
print(" is multiple of 3")
else:
print( " is not multiple of 3")
|
C#
using System;
public class GFG {
static public void Main()
{
int num = 24;
if (num % 3 == 0) {
Console.WriteLine(num+" is multiple of 3");
}
else {
Console.WriteLine(num+" is not multiple of 3");
}
}
}
|
Javascript
<script>
let num = 24;
document.write(num);
if (num % 3 == 0) {
document.write(" is multiple of 3");
}
else {
document.write(" is not multiple of 3");
}
</script>
|
Output24 is multiple of 3
Time Complexity: O(1)
Auxiliary Space: O(1)
Method 4:
1. It takes a number ‘num’ as input.
2. It calculates the digital root of the number by repeatedly adding the digits of the number until it becomes a single-digit number.
3. It then checks if the digital root is 3, 6, or 9, and returns True if it is, and False otherwise.
For example, for the number 123, the digital root would be calculated as follows:
1 + 2 + 3 = 6
Since 6 is divisible by 3, the function will return True for the input 123.
C++
#include <iostream>
#include <string>
using namespace std;
bool is_multiple_of_3(int num) {
while (num > 9) {
string num_str = to_string(num);
int sum = 0;
for (int i = 0; i < num_str.length(); i++) {
sum += num_str[i] - '0';
}
num = sum;
}
if (num % 3 == 0) {
return true;
} else {
return false;
}
}
int main() {
cout << boolalpha << is_multiple_of_3(123) << endl;
cout << boolalpha << is_multiple_of_3(789) << endl;
return 0;
}
|
Java
public class GFG {
public static boolean isMultipleOf3(int num)
{
while (num > 9) {
int sum = 0;
while (num > 0) {
sum += num % 10;
num /= 10;
}
num = sum;
}
if (num % 3 == 0) {
return true;
}
else {
return false;
}
}
public static void main(String[] args)
{
int num1 = 123;
int num2 = 789;
System.out.println(
isMultipleOf3(num1));
System.out.println(
isMultipleOf3(num2));
}
}
|
Python3
def is_multiple_of_3(num):
while num > 9:
num = sum(map(int, str(num)))
if num % 3 == 0:
return True
else:
return False
print(is_multiple_of_3(123))
print(is_multiple_of_3(789))
|
C#
using System;
namespace IsMultipleOf3 {
class Program {
static bool IsMultipleOf3(int num) {
while (num > 9) {
int sum = 0;
foreach (char c in num.ToString()) {
sum += c - '0';
}
num = sum;
}
if (num % 3 == 0) {
return true;
} else {
return false;
}
}
static void Main(string[] args) {
Console.WriteLine(IsMultipleOf3(123));
Console.WriteLine(IsMultipleOf3(789));
}
}
}
|
Javascript
function is_multiple_of_3(num) {
while (num > 9) {
let num_str = num.toString();
let sum = 0;
for (let i = 0; i < num_str.length; i++) {
sum += parseInt(num_str[i]);
}
num = sum;
}
if (num % 3 === 0) {
return true;
} else {
return false;
}
}
console.log(is_multiple_of_3(123));
console.log(is_multiple_of_3(789));
|
Time complexity: O(log n), where n is the input value
Auxiliary Space: O(1)
Related Articles:
Check divisibility in a binary stream
DFA based division
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...