Open In App
Related Articles

Program to count leaf nodes in a binary tree

Improve Article
Improve
Save Article
Save
Like Article
Like

A node is a leaf node if both left and right child nodes of it are NULL. 
Here is an algorithm to get the leaf node count.

getLeafCount(node)
1) If node is NULL then return 0.
2) Else If left and right child nodes are NULL return 1.
3) Else recursively calculate leaf count of the tree using below formula.
    Leaf count of a tree = Leaf count of left subtree + 
                                 Leaf count of right subtree

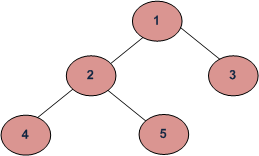
Example Tree

Leaf count for the above tree is 3.

Algorithm:

Step 1: Start
Step 2: Create a function named “getLeafCount”of int return type that take node as input parameter.
Step 3: Set the conditions:  
       a. If the node is NULL, return 0.
       b. If the node has no left or right child, return 1.
       c. Recursively call “getLeafCount” on the left and right child nodes if the node has left or right children, and then return                the total of the results.
Step 4: End

Implementation:  

C++




// C++ implementation to find leaf
// count of a given Binary tree
#include <bits/stdc++.h>
using namespace std;
 
/* A binary tree node has data,
pointer to left child and
a pointer to right child */
struct node
{
    int data;
    struct node* left;
    struct node* right;
};
 
/* Function to get the count
of leaf nodes in a binary tree*/
unsigned int getLeafCount(struct node* node)
{
    if(node == NULL)    
        return 0;
    if(node->left == NULL && node->right == NULL)
        return 1;        
    else
        return getLeafCount(node->left)+
            getLeafCount(node->right);
}
 
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
    struct node* node = (struct node*)
                    malloc(sizeof(struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
     
return(node);
}
 
/*Driver code*/
int main()
{
    /*create a tree*/
    struct node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
     
/*get leaf count of the above created tree*/
cout << "Leaf count of the tree is : "<<
                getLeafCount(root) << endl;
return 0;
}
 
// This code is contributed by SHUBHAMSINGH10

C



// C implementation to find leaf count of a given Binary tree
#include <stdio.h>
#include <stdlib.h>
 
/* A binary tree node has data, pointer to left child
   and a pointer to right child */
struct node
{
    int data;
    struct node* left;
    struct node* right;
};
 
/* Function to get the count of leaf nodes in a binary tree*/
unsigned int getLeafCount(struct node* node)
{
  if(node == NULL)      
    return 0;
  if(node->left == NULL && node->right==NULL)     
    return 1;           
  else
    return getLeafCount(node->left)+
           getLeafCount(node->right);     
}
 
/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
struct node* newNode(int data)
{
  struct node* node = (struct node*)
                       malloc(sizeof(struct node));
  node->data = data;
  node->left = NULL;
  node->right = NULL;
   
  return(node);
}
 
/*Driver program to test above functions*/ 
int main()
{
  /*create a tree*/ 
  struct node *root = newNode(1);
  root->left        = newNode(2);
  root->right       = newNode(3);
  root->left->left  = newNode(4);
  root->left->right = newNode(5);   
   
  /*get leaf count of the above created tree*/
  printf("Leaf count of the tree is %d", getLeafCount(root));
   
  getchar();
  return 0;
}
Java



// Java implementation to find leaf count of a given Binary tree
  
/* Class containing left and right child of current
 node and key value*/
class Node
{
    int data;
    Node left, right;
  
    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}
  
public class BinaryTree
{
    //Root of the Binary Tree
    Node root;
      
    /* Function to get the count of leaf nodes in a binary tree*/
    int getLeafCount()
    {
        return getLeafCount(root);
    }
  
    int getLeafCount(Node node)
    {
        if (node == null)
            return 0;
        if (node.left == null && node.right == null)
            return 1;
        else
            return getLeafCount(node.left) + getLeafCount(node.right);
    }
  
    /* Driver program to test above functions */
    public static void main(String args[])
    {
        /* create a tree */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
          
        /* get leaf count of the above tree */
        System.out.println("The leaf count of binary tree is : "
                             + tree.getLeafCount());
    }
}
 
// This code has been contributed by Mayank Jaiswal(mayank_24)
Python3



# Python program to count leaf nodes in Binary Tree
 
# A Binary tree node
class Node:
     
    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
# Function to get the count of leaf nodes in binary tree
def getLeafCount(node):
    if node is None:
        return 0
    if(node.left is None and node.right is None):
        return 1
    else:
        return getLeafCount(node.left) + getLeafCount(node.right)
 
 
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
 
print ("Leaf count of the tree is %d" %(getLeafCount(root)))
 
#This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#



using System;
 
// C# implementation to find leaf count of a given Binary tree
 
/* Class containing left and right child of current 
 node and key value*/
public class Node
{
    public int data;
    public Node left, right;
 
    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}
 
public class BinaryTree
{
    //Root of the Binary Tree
    public Node root;
 
    /* Function to get the count of leaf nodes in a binary tree*/
    public virtual int LeafCount
    {
        get
        {
            return getLeafCount(root);
        }
    }
 
    public virtual int getLeafCount(Node node)
    {
        if (node == null)
        {
            return 0;
        }
        if (node.left == null && node.right == null)
        {
            return 1;
        }
        else
        {
            return getLeafCount(node.left) + getLeafCount(node.right);
        }
    }
 
    /* Driver program to test above functions */
    public static void Main(string[] args)
    {
        /* create a tree */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
 
        /* get leaf count of the above tree */
        Console.WriteLine("The leaf count of binary tree is : " + tree.LeafCount);
    }
}
 
  // This code is contributed by Shrikant13
Javascript



<script>
    // Javascript implementation to find leaf count of a given Binary tree
     
    /* A binary tree node has data,
    pointer to left child and
    a pointer to right child */
    class node
    {
        constructor(data) {
           this.left = null;
           this.right = null;
           this.data = data;
        }
    }
     
    /* Function to get the count
    of leaf nodes in a binary tree*/
    function getLeafCount(node)
    {
        if(node == null)    
            return 0;
        if(node.left == null && node.right == null)
            return 1;        
        else
            return getLeafCount(node.left)+
                getLeafCount(node.right);
    }
 
    /* Helper function that allocates a new node with the
    given data and NULL left and right pointers. */
    function newNode(data)
    {
        let Node = new node(data);
        return(Node);
    }
     
    /*create a tree*/
    let root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
       
    /*get leaf count of the above created tree*/
    document.write("The leaf count of binary tree is : " + getLeafCount(root));
     
    // This code is contributed by mukesh07.
</script>
Output
Leaf count of the tree is : 3
Time & Space Complexities: Since this program is similar to traversal of tree, time and space complexities will be same as Tree traversal (Please see our Tree Traversal post for details) 
Another Approach(Iterative): 
The given problem can be solved by using the Level Order Traversal(https://www.geeksforgeeks.org/level-order-tree-traversal/). Follow the steps below to solve the problem:
1) Create a queue(q) and initialize count variable with 0, and store the nodes in q along wise level order and iterate for next level.
2) Perform level order traversal and check if current node is a leaf node(don’t have right and left child) then increment the count variable.
3) After completing the above steps, return count variable.
Below is the implementation of above approach:
C++



// C++ implementation to find leaf
// count of a given Binary tree
#include <bits/stdc++.h>
using namespace std;
 
// A binary tree node
struct Node{
    int data;
    struct Node* left;
    struct Node* right;
};
 
// utility function to get the new node
Node* newNode(int data){
    Node *new_node = new Node();
    new_node->data = data;
    new_node->left = NULL;
    new_node->right = NULL;
    return new_node;
}
 
// function to get count of leaf nodes
int getLeafCount(Node* root){
    // initializing queue for level order traversal
    queue<Node*> q;
    q.push(root);
    // initializing count variable
    int count = 0;
    while(!q.empty()){
        Node* temp = q.front();
        q.pop();
        if(temp->left == NULL && temp->right == NULL)
            count++;
        if(temp->left) q.push(temp->left);
        if(temp->right) q.push(temp->right);
    }
    return count;
}
 
 
// driver code to test above function
int main(){
    struct Node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
 
    // function call
    cout << "Leaf count of the tree is : "<< getLeafCount(root) << endl;
    return 0;
}
 
// THIS CODE IS CONTRIBUTED BY YASH AGARWAL(YASHAGARWAL2852002)
Java



// Java implementation to find leaf
// count of a given binary tree
import java.util.LinkedList;
import java.util.Queue;
 
// a binary tree node
class Node{
    int data;
    Node left, right;
    public Node(int item){
        data = item;
        left = null;
        right = null;
    }
}
 
class BinaryTree{
    // utility function to get the new node
    static Node newNode(int data){
        return new Node(data);
    }
     
    // function to get count of leaf nodes
    static int getLeafCount(Node root){
        // initializing queue for level order traversal
        Queue<Node> q = new LinkedList<Node>();
        q.add(root);
        // initializing count variable
        int count = 0;
        while(!q.isEmpty()){
            Node temp = q.poll();
            if(temp.left == null && temp.right == null) count++;
            if(temp.left != null) q.add(temp.left);
            if(temp.right != null) q.add(temp.right);
        }
        return count;
    }
     
    public static void main(String args[]){
        Node root = newNode(1);
        root.left = newNode(2);
        root.right = newNode(3);
        root.left.left = newNode(4);
        root.left.right = newNode(5);
         
        // function call
        System.out.println("Leaf count of the tree is : " + getLeafCount(root));
    }
}
Python



# Python program for the above approach
# structure of binary tree node
class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
     
 
# function to create a new node
def newNode(data):
    return Node(data)
 
 
# function to get count of leaf nodes
def getLeafCount(root):
    # initializing queue for level order traversal
    q = []
    q.append(root)
    # initializing count variable
    count = 0
    while(len(q) > 0):
        temp = q.pop(0)
        if(temp.left is None and temp.right is None):
            count += 1
        if(temp.left is not None):
            q.append(temp.left)
        if(temp.right is not None):
            q.append(temp.right)
    return count
 
 
# driver code to test above function
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
 
# function call
print("Leaf count of the tree is : ")
print(getLeafCount(root))
C#



// C# implementation to find leaf
// count of a given Binary tree
using System;
using System.Collections.Generic;
 
// class to represent tree node
public class Node{
  public int data;
  public Node left, right;
 
  public Node(int data){
    this.data = data;
    this.left = null;
    this.right = null;
  }
}
 
public class BinaryTree{
  // utility function to get the new node
  static Node newNode(int data){
    return new Node(data);
  }
 
  // function to get count of leaf nodes
  static int getLeafCount(Node root){
    // initializing queue for level order traversal
    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);
    int count = 0;
    while(q.Count > 0){
      Node temp = q.Dequeue();
      if(temp.left == null && temp.right == null) count++;
      if(temp.left != null) q.Enqueue(temp.left);
      if(temp.right != null) q.Enqueue(temp.right);
    }
    return count;
  }
 
  // driver program to test above function
  public static void Main(){
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
 
    // function call
    Console.WriteLine("Leaf Count of the tree is : " + getLeafCount(root));
  }
}
Javascript



// JavaScript program to find leaf
// count of a given binary tree
// a binary tree node
class Node{
    constructor(data){
        this.data = data;
        this.left = null;
        this.right = null;
    }
}
 
// utility function to get the new node
function newNode(data){
    return new Node(data);
}
 
// function to get count of leaf nodes
function getLeafCount(root){
    // initializing queue for level order traversal
    let q = [];
    q.push(root);
    // initializing count variable
    let count = 0;
    while(q.length > 0){
        let temp = q.shift();
        if(temp.left == null && temp.right == null) count++;
        if(temp.left) q.push(temp.left);
        if(temp.right) q.push(temp.right);
    }
    return count;
}
 
// driver program to test above function
let root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
 
// function call
console.log("Leaf count of the tree is : " + getLeafCount(root));
// THIS CODE IS CONTRIBUTED BY KIRTI AGARWAL(KIRTIAGARWAL23121999)
Output
Leaf count of the tree is : 3
Time Complexity: O(N) where N is the number of nodes in binary tree.
Auxiliary Space: O(N) due to queue data structure.
Please write comments if you find any bug in the above programs/algorithms or other ways to solve the same problem. 

Last Updated :
03 Apr, 2023
Like Article

Save Article

Similar Reads
Similar read thumbnail
Sum of Bitwise AND of the sum of all leaf and non-leaf nodes for each level of a Binary Tree
Similar read thumbnail
Print the longest leaf to leaf path in a Binary tree
Similar read thumbnail
Construct a Tree whose sum of nodes of all the root to leaf path is not divisible by the count of nodes in that path
Similar read thumbnail
Count of nodes in a given N-ary tree having distance to all leaf nodes equal in their subtree
Similar read thumbnail
Iterative program to count leaf nodes in a Binary Tree
Similar read thumbnail
Construct XOR tree by Given leaf nodes of Perfect Binary Tree
Similar read thumbnail
Count Non-Leaf nodes in a Binary Tree
Similar read thumbnail
Count pairs of leaf nodes in a Binary Tree which are at most K distance apart
Similar read thumbnail
Count root to leaf paths having exactly K distinct nodes in a Binary Tree
Similar read thumbnail
Count of leaf nodes required to be removed at each step to empty a given Binary Tree
Related Tutorials
Similar read thumbnail
Mathematical and Geometric Algorithms - Data Structure and Algorithm Tutorials
Similar read thumbnail
Learn Data Structures with Javascript | DSA Tutorial
Similar read thumbnail
Introduction to Max-Heap – Data Structure and Algorithm Tutorials
Similar read thumbnail
Introduction to Set – Data Structure and Algorithm Tutorials
Similar read thumbnail
Introduction to Map – Data Structure and Algorithm Tutorials
Previous
Level Order Traversal (Breadth First Search or BFS) of Binary Tree
Next

Program for array left rotation by d positions.
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Vote for difficulty
Current difficulty :
Easy





Improved By :
Article Tags :
Practice Tags :
Report Issue 
We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox