Ways of filling matrix such that product of all rows and all columns are equal to unity

We are given three values 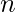, 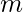and 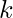where 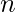is number of rows in matrix, 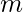is number of columns in the matrix and 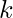is the number that can have only two values -1 and 1. Our aim is to find the number of ways of filling the matrix of such that the product of all the elements in each row and each column is equal to 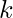. Since the number of ways can be large we will output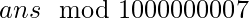 

Examples:

Input : n = 2, m = 4, k = -1
Output : 8
Following configurations satisfy the conditions:-

Input  : n = 2, m = 1, k = -1
Output : The number of filling the matrix
         are 0

From the above conditions, it is clear that the only elements that can be entered in the matrix are 1 and -1. Now we can easily deduce some of the corner cases

1. If k = -1, then the sum of number of rows and columns cannot be odd because -1 will be present odd 
   number of times in each row and column therefore if the sum is odd then answer is .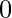
2. If n = 1 or m = 1 then there is only one way of filling the matrix therefore answer is 1.
3. If none of the above cases are applicable then we fill the first 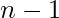rows and the first 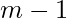columns with 1 and -1. Then the remaining numbers can be uniquely identified since the product of each row an each column is already known therefore the answer is .

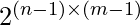Implementation:

C++

// CPP program to find number of ways to fill
// a matrix under given constraints
#include <bits/stdc++.h>
using namespace std;

#define mod 100000007

/* Returns a raised power t under modulo mod */
long long modPower(long long a, long long t)
{
    long long now = a, ret = 1;

    // Counting number of ways of filling the matrix
    while (t) {
        if (t & 1)
            ret = now * (ret % mod);
        now = now * (now % mod);
        t >>= 1;
    }
    return ret;
}

// Function calculating the answer
long countWays(int n, int m, int k)
{
    // if sum of numbers of rows and columns is odd
    // i.e (n + m) % 2 == 1 and k = -1 then there
    // are 0 ways of filiing the matrix.
    if (k == -1 && (n + m) % 2 == 1)
        return 0;

    // If there is one row or one column then there
    // is only one way of filling the matrix
    if (n == 1 || m == 1)
        return 1;

    // If the above cases are not followed then we
    // find ways to fill the n - 1 rows and m - 1
    // columns which is 2 ^ ((m-1)*(n-1)).
    return (modPower(modPower((long long)2, n - 1),
                                    m - 1) % mod);
}

// Driver function for the program
int main()
{
    int n = 2, m = 7, k = 1;
    cout << countWays(n, m, k);
    return 0;
}

Java

// Java program to find number of ways to fill
// a matrix under given constraints
import java.io.*;

class Example {

    final static long mod = 100000007;

    /* Returns a raised power t under modulo mod */
    static long modPower(long a, long t, long mod)
    {
        long now = a, ret = 1;

        // Counting number of ways of filling the
        // matrix
        while (t > 0) {
            if (t % 2 == 1)
                ret = now * (ret % mod);
            now = now * (now % mod);
            t >>= 1;
        }
        return ret;
    }

    // Function calculating the answer
    static long countWays(int n, int m, int k)
    {
        // if sum of numbers of rows and columns is
        // odd i.e (n + m) % 2 == 1 and k = -1,
        // then there are 0 ways of filiing the matrix.
        if (n == 1 || m == 1)
            return 1;

        // If there is one row or one column then
        // there is only one way of filling the matrix
        else if ((n + m) % 2 == 1 && k == -1)
            return 0;

       // If the above cases are not followed then we
       // find ways to fill the n - 1 rows and m - 1
       // columns which is 2 ^ ((m-1)*(n-1)).
        return (modPower(modPower((long)2, n - 1, mod),
                                    m - 1, mod) % mod);
    }

    // Driver function for the program
    public static void main(String args[]) throws IOException
    {
        int n = 2, m = 7, k = 1;
        System.out.println(countWays(n, m, k));
    }
}

Python3

# Python program to find number of ways to
# fill a matrix under given constraints

# Returns a raised power t under modulo mod
def modPower(a, t):

    now = a;
    ret = 1;
    mod = 100000007;

    # Counting number of ways of filling
    # the matrix
    while (t):
        if (t & 1):
            ret = now * (ret % mod);
        now = now * (now % mod);
        t >>= 1;

    return ret;

# Function calculating the answer
def countWays(n, m, k):

    mod= 100000007;

    # if sum of numbers of rows and columns
    # is odd i.e (n + m) % 2 == 1 and k = -1
    # then there are 0 ways of filiing the matrix.
    if (k == -1 and ((n + m) % 2 == 1)):
        return 0;

    # If there is one row or one column then
    # there is only one way of filling the matrix
    if (n == 1 or m == 1):
        return 1;

    # If the above cases are not followed then we
    # find ways to fill the n - 1 rows and m - 1
    # columns which is 2 ^ ((m-1)*(n-1)).
    return (modPower(modPower(2, n - 1),
                              m - 1) % mod);

# Driver Code
n = 2;
m = 7;
k = 1;
print(countWays(n, m, k));

# This code is contributed
# by Shivi_Aggarwal

C#

// C# program to find number of ways to fill
// a matrix under given constraints
using System;

class Example
{

    static long mod = 100000007;

    // Returns a raised power t
    // under modulo mod
    static long modPower(long a, long t,
                         long mod)
    {
        long now = a, ret = 1;

        // Counting number of ways
        // of filling the
        // matrix
        while (t > 0)
        {
            if (t % 2 == 1)
                ret = now * (ret % mod);
            now = now * (now % mod);
            t >>= 1;
        }
        return ret;
    }

    // Function calculating the answer
    static long countWays(int n, int m,
                          int k)
    {
        // if sum of numbers of rows
        // and columns is odd i.e
        // (n + m) % 2 == 1 and
        // k = -1, then there are 0
        // ways of filiing the matrix.
        if (n == 1 || m == 1)
            return 1;

        // If there is one row or one
        // column then there is only
        // one way of filling the matrix
        else if ((n + m) % 2 == 1 && k == -1)
            return 0;

        // If the above cases are not
        // followed then we find ways
        // to fill the n - 1 rows and
        // m - 1 columns which is
        // 2 ^ ((m-1)*(n-1)).
        return (modPower(modPower((long)2, n - 1,
                         mod), m - 1, mod) % mod);

    }

    // Driver Code
    public static void Main()
    {
        int n = 2, m = 7, k = 1;
        Console.WriteLine(countWays(n, m, k));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP program to find number
// of ways to fill a matrix under
// given constraints

$mod = 100000007;

// Returns a raised power t
// under modulo mod
function modPower($a, $t)
{
    global $mod;
    $now = $a; $ret = 1;

    // Counting number of ways
    // of filling the matrix
    while ($t)
    {
        if ($t & 1)
            $ret = $now * ($ret % $mod);
        $now = $now * ($now % $mod);
        $t >>= 1;
    }
    return $ret;
}

// Function calculating the answer
function countWays($n, $m, $k)
{
    global $mod;

    // if sum of numbers of rows
    // and columns is odd i.e
    // (n + m) % 2 == 1 and k = -1
    // then there are 0 ways of
    // filiing the matrix.
    if ($k == -1 and ($n + $m) % 2 == 1)
        return 0;

    // If there is one row or
    // one column then there
    // is only one way of
    // filling the matrix
    if ($n == 1 or $m == 1)
        return 1;

    // If the above cases are
    // not followed then we
    // find ways to fill the
    // n - 1 rows and m - 1
    // columns which is
    // 2 ^ ((m-1)*(n-1)).
    return (modPower(modPower(2, $n - 1),
                         $m - 1) % $mod);
}

    // Driver Code
    $n = 2;
    $m = 7;
    $k = 1;
    echo countWays($n, $m, $k);

// This code is contributed by anuj_67.
?>

Javascript

<script>

// JavaScript program to find number of
// ways to fill a matrix under given
// constraints

let mod = 100000007;

// Returns a raised power t under modulo mod
function modPower(a, t, mod)
{
    let now = a, ret = 1;

    // Counting number of ways of
    // filling the matrix
    while (t > 0)
    {
        if (t % 2 == 1)
            ret = now * (ret % mod);

        now = now * (now % mod);
        t >>= 1;
    }
    return ret;
}

// Function calculating the answer
function countWays(n, m, k)
{

    // If sum of numbers of rows and columns is
    // odd i.e (n + m) % 2 == 1 and k = -1,
    // then there are 0 ways of filiing the matrix.
    if (n == 1 || m == 1)
        return 1;

    // If there is one row or one column then
    // there is only one way of filling the matrix
    else if ((n + m) % 2 == 1 && k == -1)
        return 0;

   // If the above cases are not followed then we
   // find ways to fill the n - 1 rows and m - 1
   // columns which is 2 ^ ((m-1)*(n-1)).
    return (modPower(modPower(2, n - 1, mod),
                                 m - 1, mod) % mod);
}

// Driver Code
let n = 2, m = 7, k = 1;

document.write(countWays(n, m, k));

// This code is contributed by code_hunt

</script>

Output:

64

Time complexity: 

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

.
Space Complexity : O(1).