Selection Sort – Data Structure and Algorithm Tutorials
Last Updated :
17 Apr, 2024
Selection sort is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list.
The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion of the list and swaps it with the first element of the unsorted part. This process is repeated for the remaining unsorted portion until the entire list is sorted.
How does Selection Sort Algorithm work?
Lets consider the following array as an example: arr[] = {64, 25, 12, 22, 11}
First pass:
- For the first position in the sorted array, the whole array is traversed from index 0 to 4 sequentially. The first position where 64 is stored presently, after traversing whole array it is clear that 11 is the lowest value.
- Thus, replace 64 with 11. After one iteration 11, which happens to be the least value in the array, tends to appear in the first position of the sorted list.
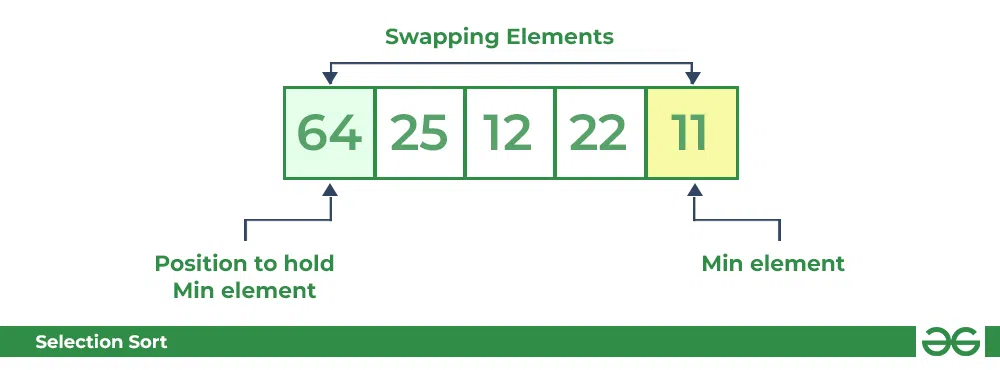
Selection Sort Algorithm | Swapping 1st element with the minimum in array
Second Pass:
- For the second position, where 25 is present, again traverse the rest of the array in a sequential manner.
- After traversing, we found that 12 is the second lowest value in the array and it should appear at the second place in the array, thus swap these values.
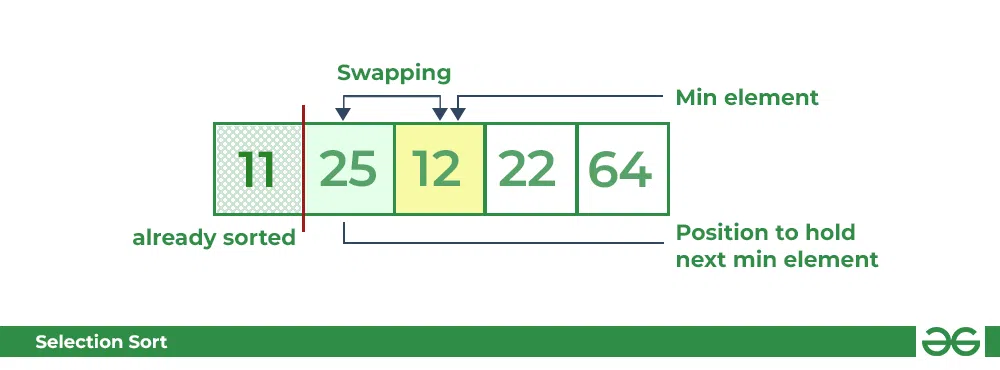
Selection Sort Algorithm | swapping i=1 with the next minimum element
Third Pass:
- Now, for third place, where 25 is present again traverse the rest of the array and find the third least value present in the array.
- While traversing, 22 came out to be the third least value and it should appear at the third place in the array, thus swap 22 with element present at third position.
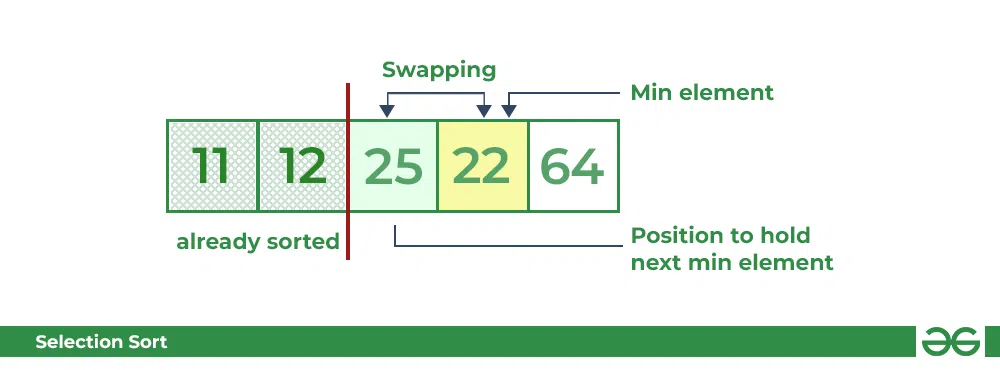
Selection Sort Algorithm | swapping i=2 with the next minimum element
Fourth pass:
- Similarly, for fourth position traverse the rest of the array and find the fourth least element in the array
- As 25 is the 4th lowest value hence, it will place at the fourth position.
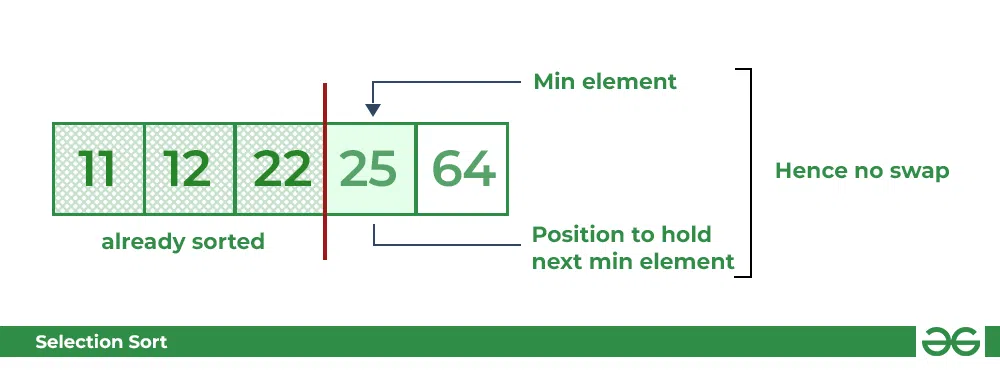
Selection Sort Algorithm | swapping i=3 with the next minimum element
Fifth Pass:
- At last the largest value present in the array automatically get placed at the last position in the array
- The resulted array is the sorted array.
Selection Sort Algorithm | Required sorted array
Below is the implementation of the above approach:
C++
// C++ program for implementation of
// selection sort
#include <bits/stdc++.h>
using namespace std;
// Function for Selection sort
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of
// unsorted subarray
for (i = 0; i < n - 1; i++) {
// Find the minimum element in
// unsorted array
min_idx = i;
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[min_idx])
min_idx = j;
}
// Swap the found minimum element
// with the first element
if (min_idx != i)
swap(arr[min_idx], arr[i]);
}
}
// Function to print an array
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++) {
cout << arr[i] << " ";
cout << endl;
}
}
// Driver program
int main()
{
int arr[] = { 64, 25, 12, 22, 11 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function Call
selectionSort(arr, n);
cout << "Sorted array: \n";
printArray(arr, n);
return 0;
}
// This is code is contributed by rathbhupendra
// C program for implementation of selection sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
if(min_idx != i)
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
// Java program for implementation of Selection Sort
import java.io.*;
public class SelectionSort
{
void sort(int arr[])
{
int n = arr.length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first
// element
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
// Prints the array
void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i]+" ");
System.out.println();
}
// Driver code to test above
public static void main(String args[])
{
SelectionSort ob = new SelectionSort();
int arr[] = {64,25,12,22,11};
ob.sort(arr);
System.out.println("Sorted array");
ob.printArray(arr);
}
}
/* This code is contributed by Rajat Mishra*/
# Python program for implementation of Selection
# Sort
A = [64, 25, 12, 22, 11]
# Traverse through all array elements
for i in range(len(A)-1):
# Find the minimum element in remaining
# unsorted array
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
# Swap the found minimum element with
# the first element
A[i], A[min_idx] = A[min_idx], A[i]
# Driver code to test above
print ("Sorted array")
for i in range(len(A)):
print(A[i],end=" ")
// C# program for implementation
// of Selection Sort
using System;
class GFG
{
static void sort(int []arr)
{
int n = arr.Length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n - 1; i++)
{
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first
// element
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
// Prints the array
static void printArray(int []arr)
{
int n = arr.Length;
for (int i=0; i<n; ++i)
Console.Write(arr[i]+" ");
Console.WriteLine();
}
// Driver code
public static void Main()
{
int []arr = {64,25,12,22,11};
sort(arr);
Console.WriteLine("Sorted array");
printArray(arr);
}
}
// This code is contributed by Sam007
<script>
// Javascript program for implementation of selection sort
function swap(arr,xp, yp)
{
var temp = arr[xp];
arr[xp] = arr[yp];
arr[yp] = temp;
}
function selectionSort(arr, n)
{
var i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(arr,min_idx, i);
}
}
function printArray( arr, size)
{
var i;
for (i = 0; i < size; i++)
document.write(arr[i] + " ");
document.write(" <br>");
}
var arr = [64, 25, 12, 22, 11];
var n = 5;
selectionSort(arr, n);
document.write("Sorted array: <br>");
printArray(arr, n);
// This code is contributed by akshitsaxenaa09.
</script>
<?php
// PHP program for implementation
// of selection sort
function selection_sort(&$arr, $n)
{
for($i = 0; $i < $n ; $i++)
{
$low = $i;
for($j = $i + 1; $j < $n ; $j++)
{
if ($arr[$j] < $arr[$low])
{
$low = $j;
}
}
// swap the minimum value to $ith node
if ($arr[$i] > $arr[$low])
{
$tmp = $arr[$i];
$arr[$i] = $arr[$low];
$arr[$low] = $tmp;
}
}
}
// Driver Code
$arr = array(64, 25, 12, 22, 11);
$len = count($arr);
selection_sort($arr, $len);
echo "Sorted array : \n";
for ($i = 0; $i < $len; $i++)
echo $arr[$i] . " ";
// This code is contributed
// by Deepika Gupta.
?>
OutputSorted array:
11 12 22 25 64
Complexity Analysis of Selection Sort
Time Complexity: The time complexity of Selection Sort is O(N2) as there are two nested loops:
- One loop to select an element of Array one by one = O(N)
- Another loop to compare that element with every other Array element = O(N)
- Therefore overall complexity = O(N) * O(N) = O(N*N) = O(N2)
Auxiliary Space: O(1) as the only extra memory used is for temporary variables while swapping two values in Array. The selection sort never makes more than O(N) swaps and can be useful when memory writing is costly.
Advantages of Selection Sort Algorithm
- Simple and easy to understand.
- Works well with small datasets.
Disadvantages of the Selection Sort Algorithm
- Selection sort has a time complexity of O(n^2) in the worst and average case.
- Does not work well on large datasets.
- Does not preserve the relative order of items with equal keys which means it is not stable.
Frequently Asked Questions on Selection Sort
Q1. Is Selection Sort Algorithm stable?
The default implementation of the Selection Sort Algorithm is not stable. However, it can be made stable. Please see the stable Selection Sort for details.
Q2. Is Selection Sort Algorithm in-place?
Yes, Selection Sort Algorithm is an in-place algorithm, as it does not require extra space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...