Naive algorithm for Pattern Searching

Given text string with length n and a pattern with length m, the task is to prints all occurrences of pattern in text.
Note: You may assume that n > m.

Examples:

Input:  text = “THIS IS A TEST TEXT”, pattern = “TEST”
Output: Pattern found at index 10

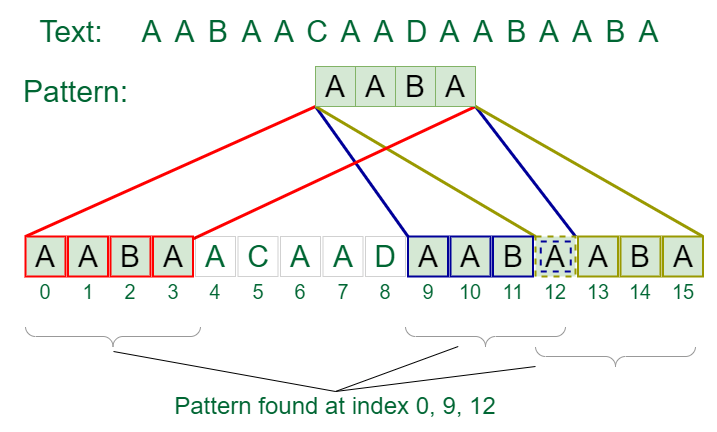
Input:  text =  “AABAACAADAABAABA”, pattern = “AABA”
Output: Pattern found at index 0, Pattern found at index 9, Pattern found at index 12

Pattern searching

Naive Pattern Searching algorithm:

Slide the pattern over text one by one and check for a match. If a match is found, then slide by 1 again to check for subsequent matches. 

C++

#include <iostream>
#include <string>
using namespace std;

void search(string& pat, string& txt) {
    int M = pat.size();
    int N = txt.size();

    // A loop to slide pat[] one by one
    for (int i = 0; i <= N - M; i++) {
        int j;

        // For current index i, check for pattern match
        for (j = 0; j < M; j++) {
            if (txt[i + j] != pat[j]) {
                break;
            }
        }

        // If pattern matches at index i
        if (j == M) {
            cout << "Pattern found at index " << i << endl;
        }
    }
}

// Driver's Code
int main() {
    // Example 1
    string txt1 = "AABAACAADAABAABA";
    string pat1 = "AABA";
    cout << "Example 1: " << endl;
    search(pat1, txt1);
    
    // Example 2
    string txt2 = "agd";
    string pat2 = "g";
    cout << "\nExample 2: " << endl;
    search(pat2, txt2);

    return 0;
}

C

#include <stdio.h>
#include <string.h>

void search(char* pat, char* txt) {
    int M = strlen(pat);
    int N = strlen(txt);

    // A loop to slide pat[] one by one
    for (int i = 0; i <= N - M; i++) {
        int j;

        // For current index i, check for pattern match
        for (j = 0; j < M; j++) {
            if (txt[i + j] != pat[j]) {
                break;
            }
        }

        // If pattern matches at index i
        if (j == M) {
            printf("Pattern found at index %d\n", i);
        }
    }
}

int main() {
    // Example 1
    char txt1[] = "AABAACAADAABAABA";
    char pat1[] = "AABA";
    printf("Example 1:\n");
    search(pat1, txt1);
    
    // Example 2
    char txt2[] = "agd";
    char pat2[] = "g";
    printf("\nExample 2:\n");
    search(pat2, txt2);

    return 0;
}

Java

public class PatternSearch {

    public static void search(String pat, String txt) {
        int M = pat.length();
        int N = txt.length();

        // A loop to slide pat[] one by one
        for (int i = 0; i <= N - M; i++) {
            int j;

            // For current index i, check for pattern match
            for (j = 0; j < M; j++) {
                if (txt.charAt(i + j) != pat.charAt(j)) {
                    break;
                }
            }

            // If pattern matches at index i
            if (j == M) {
                System.out.println("Pattern found at index " + i);
            }
        }
    }

    public static void main(String[] args) {
        // Example 1
        String txt1 = "AABAACAADAABAABA";
        String pat1 = "AABA";
        System.out.println("Example 1:");
        search(pat1, txt1);

        // Example 2
        String txt2 = "agd";
        String pat2 = "g";
        System.out.println("\nExample 2:");
        search(pat2, txt2);
    }
}

Python3

def search_pattern(pattern, text):
    # Get the lengths of the pattern and the text
    m = len(pattern)
    n = len(text)

    # A loop to slide pattern over text one by one
    for i in range(n - m + 1):
        # For current index i, check for pattern match
        j = 0
        while j < m and text[i + j] == pattern[j]:
            j += 1
        
        # If the entire pattern matches the text starting at index i
        if j == m:
            print(f"Pattern found at index {i}")

# Example usage
if __name__ == "__main__":
    # Example 1
    text1 = "AABAACAADAABAABA"
    pattern1 = "AABA"
    print("Example 1:")
    search_pattern(pattern1, text1)
    
    # Example 2
    text2 = "agd"
    pattern2 = "g"
    print("\nExample 2:")
    search_pattern(pattern2, text2)

C#

using System;

class PatternSearch
{
    static void Search(string pat, string txt)
    {
        int M = pat.Length;
        int N = txt.Length;

        // A loop to slide pat[] one by one
        for (int i = 0; i <= N - M; i++)
        {
            int j;

            // For current index i, check for pattern match
            for (j = 0; j < M; j++)
            {
                if (txt[i + j] != pat[j])
                {
                    break;
                }
            }

            // If pattern matches at index i
            if (j == M)
            {
                Console.WriteLine($"Pattern found at index {i}");
            }
        }
    }

    static void Main()
    {
        // Example 1
        string txt1 = "AABAACAADAABAABA";
        string pat1 = "AABA";
        Console.WriteLine("Example 1:");
        Search(pat1, txt1);
        
        // Example 2
        string txt2 = "agd";
        string pat2 = "g";
        Console.WriteLine("\nExample 2:");
        Search(pat2, txt2);
    }
}

Javascript

   function search(pat, txt) {
    const M = pat.length;
    const N = txt.length;

    // A loop to slide pat[] one by one
    for (let i = 0; i <= N - M; i++) {
        let j = 0;

        // For current index i, check for pattern match
        while (j < M && txt[i + j] === pat[j]) {
            j++;
        }

        // If pattern matches at index i
        if (j === M) {
            console.log(`Pattern found at index ${i}`);
        }
    }
}

// Example 1
const txt1 = "AABAACAADAABAABA";
const pat1 = "AABA";
console.log("Example 1:");
search(pat1, txt1);

// Example 2
const txt2 = "agd";
const pat2 = "g";
console.log("\nExample 2:");
search(pat2, txt2);

PHP

function search($pat, $txt) {
    $M = strlen($pat);
    $N = strlen($txt);

    // A loop to slide pat[] one by one
    for ($i = 0; $i <= $N - $M; $i++) {
        $j = 0;

        // For current index i, check for pattern match
        while ($j < $M && $txt[$i + $j] === $pat[$j]) {
            $j++;
        }

        // If pattern matches at index i
        if ($j == $M) {
            echo "Pattern found at index $i\n";
        }
    }
}

// Example 1
$txt1 = "AABAACAADAABAABA";
$pat1 = "AABA";
echo "Example 1:\n";
search($pat1, $txt1);

// Example 2
$txt2 = "agd";
$pat2 = "g";
echo "\nExample 2:\n";
search($pat2, $txt2);

Output

Pattern found at index 0 
Pattern found at index 9 
Pattern found at index 13 

Time Complexity: O(N²)
Auxiliary Space: O(1)

Complexity Analysis of Naive algorithm for Pattern Searching:

Best Case: O(n)

• When the pattern is found at the very beginning of the text (or very early on).
• The algorithm will perform a constant number of comparisons, typically on the order of O(n) comparisons, where n is the length of the pattern.

Worst Case: O(n²)

• When the pattern doesn’t appear in the text at all or appears only at the very end.
• The algorithm will perform O((n-m+1)*m) comparisons, where n is the length of the text and m is the length of the pattern.
• In the worst case, for each position in the text, the algorithm may need to compare the entire pattern against the text.