Root to leaf path sum equal to a given number

Given a binary tree and a number, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals the given number. Return false if no such path can be found. 

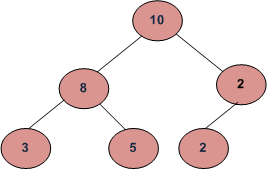
For example, in the above tree root to leaf paths exist with the following sums.
21 –> 10 – 8 – 3 
23 –> 10 – 8 – 5 
14 –> 10 – 2 – 2
So the returned value should be true only for numbers 21, 23, and 14. For any other number, the returned value should be false.

Algorithm: 
Recursively check if left or right child has path sum equal to ( number – value at the current node)
Implementation:  

C++

#include <bits/stdc++.h>
using namespace std;
#define bool int

/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node
{
    public:
    int data;
    node* left;
    node* right;
};

/*
Given a tree and a sum, return true if there is a path from the root
down to a leaf, such that adding up all the values along the path
equals the given sum.

Strategy: subtract the node value from the sum when recurring down,
and check to see if the sum is 0 when you when you reach the leaf node.
*/
bool hasPathSum(node* Node, int sum)
{
    if(Node==NULL)
      return 0;

  bool ans = 0;

  int subSum = sum - Node->data;

  /* If we reach a leaf node and sum becomes 0 then return true*/
  if ( subSum == 0 && Node->left == NULL && Node->right == NULL )
    return 1;

  /* otherwise check both subtrees */
  if(Node->left)
    ans = ans || hasPathSum(Node->left, subSum);
  if(Node->right)
    ans = ans || hasPathSum(Node->right, subSum);

  return ans;

}

/* UTILITY FUNCTIONS */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newnode(int data)
{
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;

    return(Node);
}

// Driver Code
int main()
{

    int sum = 21;

    /* Constructed binary tree is
                10
            / \
            8 2
        / \ /
        3 5 2
    */
    node *root = newnode(10);
    root->left = newnode(8);
    root->right = newnode(2);
    root->left->left = newnode(3);
    root->left->right = newnode(5);
    root->right->left = newnode(2);

    if(hasPathSum(root, sum))
        cout << "There is a root-to-leaf path with sum " << sum;
    else
        cout << "There is no root-to-leaf path with sum " << sum;

    return 0;
}

// This code is contributed by rathbhupendra

C

#include <stdio.h>
#include <stdlib.h>
#define bool int

/* A binary tree node has data, pointer to left child
   and a pointer to right child */
struct node {
    int data;
    struct node* left;
    struct node* right;
};

/*
 Given a tree and a sum, return
 true if there is a path from
 the root down to a leaf, such
 that adding up all the values
 along the path equals the given sum.

 Strategy: subtract the node
 value from the sum when
 recurring down, and check to
 see if the sum is 0 when you reach the leaf node.
*/
bool hasPathSum(struct node* node, int sum)
{
  if(node==NULL)
    return 0;
  bool ans = 0;

  int subSum = sum - node->data;

  /* If we reach a leaf node
        and sum becomes 0 then
         * return true*/
  if (subSum == 0 && node->left == NULL
      && node->right == NULL)
    return 1;

  /* otherwise check both subtrees */
  if (node->left)
    ans = ans
    || hasPathSum(node->left, subSum);
  if (node->right)
    ans = ans
    || hasPathSum(node->right, subSum);

  return ans;

}

/* UTILITY FUNCTIONS */
/* Helper function that
   allocates a new node with the
   given data and NULL left
   and right pointers. */
struct node* newnode(int data)
{
    struct node* node
        = (struct node*)malloc(sizeof(struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;

    return (node);
}

// Driver Code
int main()
{

    int sum = 21;

    /* Constructed binary tree is
              10
            /   \
          8      2
        /  \    /
      3     5  2
    */
    struct node* root = newnode(10);
    root->left = newnode(8);
    root->right = newnode(2);
    root->left->left = newnode(3);
    root->left->right = newnode(5);
    root->right->left = newnode(2);

    if (hasPathSum(root, sum))
        printf("There is a root-to-leaf path with sum %d",
               sum);
    else
        printf("There is no root-to-leaf path with sum %d",
               sum);

    getchar();
    return 0;
}

Java

// Java program to print
// root to leaf path sum
// equal to a given number

/* A binary tree node has data,
 pointer to left child
   and a pointer to right child */
class Node {
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class BinaryTree {

    Node root;

    /*
     Given a tree and a sum,
     return true if there is a path
     from the root down to a leaf,
     such that adding up all
     the values along the path
     equals the given sum.

     Strategy: subtract the node
     value from the sum when
     recurring down, and check to
     see if the sum is 0 you reach the leaf node.
     */

    boolean hasPathSum(Node node, int sum)
    { /* If the tree is empty there is no way the reqd sum will be there. */
      if(root==null)
      return false;
      boolean ans = false;
      int subSum = sum - node.data;
      if(subSum == 0 && node.left == null && node.right == null)
        return(ans = true);
      if(node.left != null)

        // ans || hasPathSum... has no utility if the ans is false
        ans = ans || hasPathSum(node.left, subSum);

      if(node.right != null)

        // But if it is true then we can avoid calling hasPathSum
        // here as answer has already been found
        ans = ans || hasPathSum(node.right, subSum);
      return(ans);
    }

    // Driver Code
    public static void main(String args[])
    {
        int sum = 21;

        /* Constructed binary tree is
              10
             /  \
           8     2
          / \   /
         3   5 2
        */
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(8);
        tree.root.right = new Node(2);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(2);

        if (tree.hasPathSum(tree.root, sum))
            System.out.println(
                "There is a root to leaf path with sum "
                + sum);
        else
            System.out.println(
                "There is no root to leaf path with sum "
                + sum);
    }
}

// This code has been contributed by Mayank
// Jaiswal(mayank_24)

Python3

# Python program to find if
# there is a root to sum path

# A binary tree node


class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None


"""
 Given a tree and a sum, return
 true if there is a path from the root
 down to a leaf, such that
 adding up all the values along the path
 equals the given sum.

 Strategy: subtract the node
 value from the sum when recurring down,
 and check to see if the sum
 is 0 when you run out of tree.
"""
# s is the sum


def hasPathSum(node, s):
        ans = 0
        subSum = s - node.data

        # If we reach a leaf node and sum becomes 0, then
        # return True
        if(subSum == 0 and node.left == None and node.right == None):
            return True

        # Otherwise check both subtrees
        if node.left is not None:
            ans = ans or hasPathSum(node.left, subSum)
        if node.right is not None:
            ans = ans or hasPathSum(node.right, subSum)

        return ans

# Driver Code


s = 21
root = Node(10)
root.left = Node(8)
root.right = Node(2)
root.left.right = Node(5)
root.left.left = Node(3)
root.right.left = Node(2)

if hasPathSum(root, s):
    print("There is a root-to-leaf path with sum %d" % (s))
else:
    print("There is no root-to-leaf path with sum %d" % (s))

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// C# program to print root to
// leaf path sum equal to a given number
using System;

/* A binary tree node has data, pointer
to left child and a pointer to right child */
public class Node {
    public int data;
    public Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class GFG {
    public Node root;

    /*
    Given a tree and a sum, return true if
    there is a path from the root down to a
    leaf, such that adding up all the values
    along the path equals the given sum.

    Strategy: subtract the node value from the
    sum when recurring down, and check to see
    if the sum is 0 when you you reach the leaf node..
    */

    public virtual bool haspathSum(Node node, int sum)
    {
        ans = false;

        int subsum = sum - node.data;
        if (subsum == 0 && node.left == null
            && node.right == null) {
            return true;
        }

        /* otherwise check both subtrees */
        if (node.left != null) {
            ans = ans || haspathSum(node.left, subsum);
        }
        if (node.right != null) {
            ans = ans || haspathSum(node.right, subsum);
        }
        return ans;
    }

    // Driver Code
    public static void Main(string[] args)
    {
        int sum = 21;

        /* Constructed binary tree is
            10
            / \
        8     2
        / \ /
        3 5 2
        */
        GFG tree = new GFG();
        tree.root = new Node(10);
        tree.root.left = new Node(8);
        tree.root.right = new Node(2);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(2);

        if (tree.haspathSum(tree.root, sum)) {
            Console.WriteLine("There is a root to leaf "
                              + "path with sum " + sum);
        }
        else {
            Console.WriteLine("There is no root to leaf "
                              + "path with sum " + sum);
        }
    }
}

// This code is contributed by Shrikant13

Javascript

<script>
// javascript program to print
// root to leaf path sum
// equal to a given number

/* A binary tree node has data,
 pointer to left child
   and a pointer to right child */

class Node {
        constructor(val) {
            this.data = val;
            this.left = null;
            this.right = null;
        }
    }

var root;

    /*
     Given a tree and a sum,
     return true if there is a path
     from the root down to a leaf,
     such that adding up all
     the values along the path
     equals the given sum.

     Strategy: subtract the node
     value from the sum when
     recurring down, and check to
     see if the sum is 0 you reach the leaf node.
     */

    function hasPathSum(node , sum)
    {
      var ans = false;
      var subSum = sum - node.data;
      if(subSum == 0 && node.left == null && node.right == null)
        return(ans = true);
      if(node.left != null)

        // ans || hasPathSum... has no utility if the ans is false
        ans = ans || hasPathSum(node.left, subSum);

      if(node.right != null)

        // But if it is true then we can afunction calling hasPathSum
        // here as answer has already been found
        ans = ans || hasPathSum(node.right, subSum);
      return(ans);
    }

    // Driver Code

        var sum = 21;

        /* Constructed binary tree is
              10
             /  \
           8     2
          / \   /
         3   5 2
        */

        var root = new Node(10);
        root.left = new Node(8);
        root.right = new Node(2);
        root.left.left = new Node(3);
        root.left.right = new Node(5);
        root.right.left = new Node(2);

        if (hasPathSum(root, sum))
            document.write(
                "There is a root to leaf path with sum "
                + sum);
        else
            document.write(
                "There is no root to leaf path with sum "
                + sum);

// This code is contributed by gauravrajput1
</script>

Output

There is a root-to-leaf path with sum 21

Time Complexity: O(n)

Auxiliary Space: O(n)

References: http://cslibrary.stanford.edu/110/BinaryTrees.html
Author: Tushar Roy

Please write comments if you find any bug in above code/algorithm, or find other ways to solve the same problem