Radix Sort – Data Structures and Algorithms Tutorials
Last Updated :
19 Apr, 2024
Radix Sort is a linear sorting algorithm that sorts elements by processing them digit by digit. It is an efficient sorting algorithm for integers or strings with fixed-size keys.
Rather than comparing elements directly, Radix Sort distributes the elements into buckets based on each digit’s value. By repeatedly sorting the elements by their significant digits, from the least significant to the most significant, Radix Sort achieves the final sorted order.
Radix Sort Algorithm
The key idea behind Radix Sort is to exploit the concept of place value. It assumes that sorting numbers digit by digit will eventually result in a fully sorted list. Radix Sort can be performed using different variations, such as Least Significant Digit (LSD) Radix Sort or Most Significant Digit (MSD) Radix Sort.
How does Radix Sort Algorithm work?
To perform radix sort on the array [170, 45, 75, 90, 802, 24, 2, 66], we follow these steps:

How does Radix Sort Algorithm work | Step 1
Step 1: Find the largest element in the array, which is 802. It has three digits, so we will iterate three times, once for each significant place.
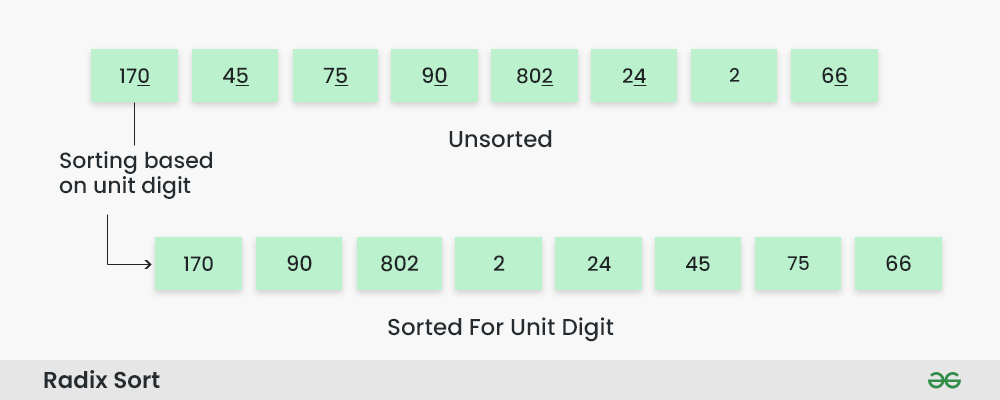
Step 2: Sort the elements based on the unit place digits (X=0). We use a stable sorting technique, such as counting sort, to sort the digits at each significant place.
Sorting based on the unit place:
- Perform counting sort on the array based on the unit place digits.
- The sorted array based on the unit place is [170, 90, 802, 2, 24, 45, 75, 66].
How does Radix Sort Algorithm work | Step 2
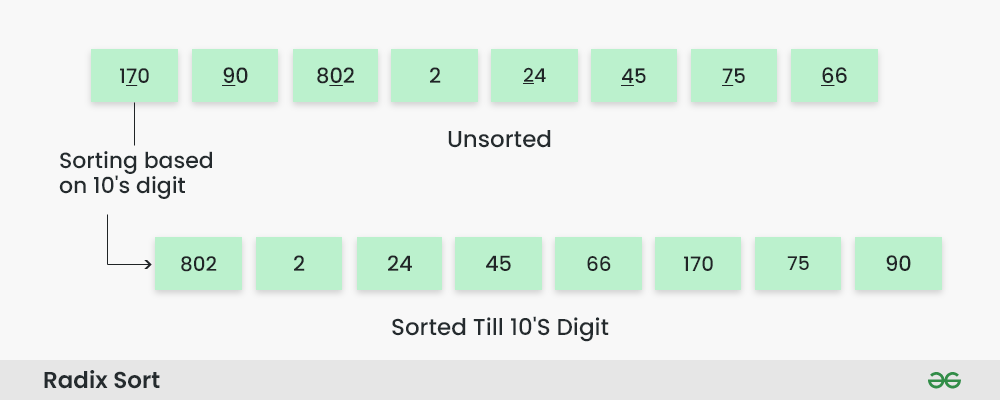
Step 3: Sort the elements based on the tens place digits.
Sorting based on the tens place:
- Perform counting sort on the array based on the tens place digits.
- The sorted array based on the tens place is [802, 2, 24, 45, 66, 170, 75, 90].
How does Radix Sort Algorithm work | Step 3
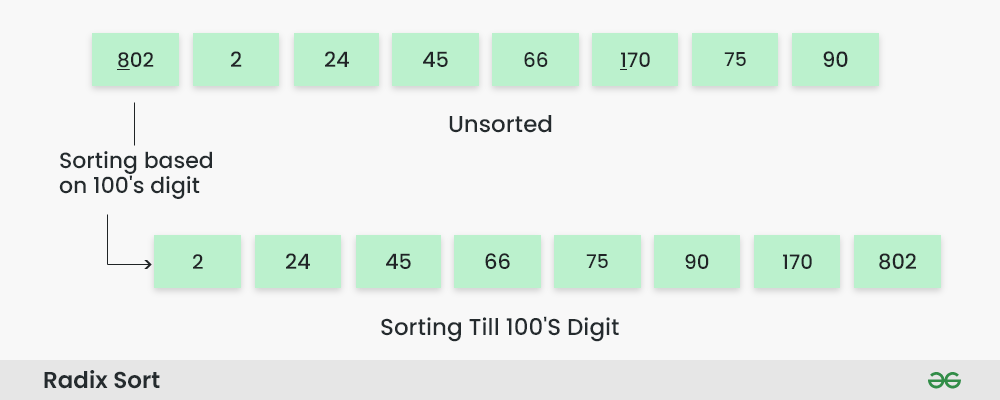
Step 4: Sort the elements based on the hundreds place digits.
Sorting based on the hundreds place:
- Perform counting sort on the array based on the hundreds place digits.
- The sorted array based on the hundreds place is [2, 24, 45, 66, 75, 90, 170, 802].
How does Radix Sort Algorithm work | Step 4
Step 5: The array is now sorted in ascending order.
The final sorted array using radix sort is [2, 24, 45, 66, 75, 90, 170, 802].

How does Radix Sort Algorithm work | Step 5
Below is the implementation for the above illustrations:
C++
// C++ implementation of Radix Sort
#include <iostream>
using namespace std;
// A utility function to get maximum
// value in arr[]
int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[]
// according to the digit
// represented by exp.
void countSort(int arr[], int n, int exp)
{
// Output array
int output[n];
int i, count[10] = { 0 };
// Store count of occurrences
// in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i]
// now contains actual position
// of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[],
// so that arr[] now contains sorted
// numbers according to current digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[]
// of size n using Radix Sort
void radixsort(int arr[], int n)
{
// Find the maximum number to
// know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit.
// Note that instead of passing digit
// number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
// Driver Code
int main()
{
int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function Call
radixsort(arr, n);
print(arr, n);
return 0;
}
// Radix sort Java implementation
import java.io.*;
import java.util.*;
class Radix {
// A utility function to get maximum value in arr[]
static int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
static void countSort(int arr[], int n, int exp)
{
int output[] = new int[n]; // output array
int i;
int count[] = new int[10];
Arrays.fill(count, 0);
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains
// actual position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current
// digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of
// size n using Radix Sort
static void radixsort(int arr[], int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
static void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
// Main driver method
public static void main(String[] args)
{
int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = arr.length;
// Function Call
radixsort(arr, n);
print(arr, n);
}
}
# Python program for implementation of Radix Sort
# A function to do counting sort of arr[] according to
# the digit represented by exp.
def countingSort(arr, exp1):
n = len(arr)
# The output array elements that will have sorted arr
output = [0] * (n)
# initialize count array as 0
count = [0] * (10)
# Store count of occurrences in count[]
for i in range(0, n):
index = arr[i] // exp1
count[index % 10] += 1
# Change count[i] so that count[i] now contains actual
# position of this digit in output array
for i in range(1, 10):
count[i] += count[i - 1]
# Build the output array
i = n - 1
while i >= 0:
index = arr[i] // exp1
output[count[index % 10] - 1] = arr[i]
count[index % 10] -= 1
i -= 1
# Copying the output array to arr[],
# so that arr now contains sorted numbers
i = 0
for i in range(0, len(arr)):
arr[i] = output[i]
# Method to do Radix Sort
def radixSort(arr):
# Find the maximum number to know number of digits
max1 = max(arr)
# Do counting sort for every digit. Note that instead
# of passing digit number, exp is passed. exp is 10^i
# where i is current digit number
exp = 1
while max1 / exp >= 1:
countingSort(arr, exp)
exp *= 10
# Driver code
arr = [170, 45, 75, 90, 802, 24, 2, 66]
# Function Call
radixSort(arr)
for i in range(len(arr)):
print(arr[i], end=" ")
# This code is contributed by Mohit Kumra
# Edited by Patrick Gallagher
// C# implementation of Radix Sort
using System;
class GFG {
public static int getMax(int[] arr, int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
public static void countSort(int[] arr, int n, int exp)
{
int[] output = new int[n]; // output array
int i;
int[] count = new int[10];
// initializing all elements of count to 0
for (i = 0; i < 10; i++)
count[i] = 0;
// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] now contains
// actual
// position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current
// digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using
// Radix Sort
public static void radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
// A utility function to print an array
public static void print(int[] arr, int n)
{
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
// Driver Code
public static void Main()
{
int[] arr = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = arr.Length;
// Function Call
radixsort(arr, n);
print(arr, n);
}
// This code is contributed by DrRoot_
}
// Radix sort JavaScript implementation
"use strict";
// A utility function to get maximum value in arr[]
function getMax(arr) {
const length = arr.length;
let mx = arr[0];
for (let i = 1; i < length; i++) {
if (arr[i] > mx) mx = arr[i];
}
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
function countSort(arr, exp) {
const length = arr.length;
let output = Array(length); // output array
let count = Array(10).fill(0, 0);
// Store count of occurrences in count[]
for (let i = 0; i < length; i++) {
const digit = Math.floor(arr[i] / exp) % 10;
count[digit]++;
}
// Change count[i] so that count[i] now contains
// actual position of this digit in output[]
for (let i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// Build the output array
for (let i = length - 1; i >= 0; i--) {
const digit = Math.floor(arr[i] / exp) % 10;
output[count[digit] - 1] = arr[i];
count[digit]--;
}
return output;
}
// The main function to that sorts arr[] using Radix Sort
function radixSort(arr) {
// Find the maximum number to know number of digits
const maxNumber = getMax(arr);
// Create a shallow copy where the sorted values will be kept
let sortedArr = [...arr];
// Do counting sort for every digit. Note that
// instead of passing digit number, exp is passed.
// exp is 10^i where i is current digit number
for (let exp = 1; Math.floor(maxNumber / exp) > 0; exp *= 10) {
// Get the Count sort iteration
const sortedIteration = countSort(sortedArr, exp);
sortedArr = sortedIteration;
}
return sortedArr;
}
/*Driver Code*/
const arr = [170, 45, 75, 90, 802, 24, 2, 66];
// Function Call
const sortedArr = radixSort(arr);
console.log(sortedArr.join(" "));
// This code is contributed by beeduhboodee
<?php
// PHP implementation of Radix Sort
// A function to do counting sort of arr[]
// according to the digit represented by exp.
function countSort(&$arr, $n, $exp)
{
$output = array_fill(0, $n, 0); // output array
$count = array_fill(0, 10, 0);
// Store count of occurrences in count[]
for ($i = 0; $i < $n; $i++)
$count[ ($arr[$i] / $exp) % 10 ]++;
// Change count[i] so that count[i]
// now contains actual position of
// this digit in output[]
for ($i = 1; $i < 10; $i++)
$count[$i] += $count[$i - 1];
// Build the output array
for ($i = $n - 1; $i >= 0; $i--)
{
$output[$count[ ($arr[$i] /
$exp) % 10 ] - 1] = $arr[$i];
$count[ ($arr[$i] / $exp) % 10 ]--;
}
// Copy the output array to arr[], so
// that arr[] now contains sorted numbers
// according to current digit
for ($i = 0; $i < $n; $i++)
$arr[$i] = $output[$i];
}
// The main function to that sorts arr[]
// of size n using Radix Sort
function radixsort(&$arr, $n)
{
// Find the maximum number to know
// number of digits
$m = max($arr);
// Do counting sort for every digit. Note
// that instead of passing digit number,
// exp is passed. exp is 10^i where i is
// current digit number
for ($exp = 1; $m / $exp > 0; $exp *= 10)
countSort($arr, $n, $exp);
}
// A utility function to print an array
function PrintArray(&$arr,$n)
{
for ($i = 0; $i < $n; $i++)
echo $arr[$i] . " ";
}
// Driver Code
$arr = array(170, 45, 75, 90, 802, 24, 2, 66);
$n = count($arr);
// Function Call
radixsort($arr, $n);
PrintArray($arr, $n);
// This code is contributed by rathbhupendra
?>
// Radix sort Dart implementation
/// A utility function to get the maximum value of a `List<int>` [array]
int getMax(List<int> array) {
int max = array[0];
for (final it in array) {
if (it > max) {
max = it;
}
}
return max;
}
/// A function to do counting sort of `List<int>` [array] according to the
/// digit represented by [exp].
List<int> countSort(List<int> array, int exp) {
final length = array.length;
final outputArr = List.filled(length, 0);
// A list where index represents the digit and value represents the count of
// occurrences
final digitsCount = List.filled(10, 0);
// Store count of occurrences in digitsCount[]
for (final item in array) {
final digit = item ~/ exp % 10;
digitsCount[digit]++;
}
// Change digitsCount[i] so that digitsCount[i] now contains actual position
// of this digit in outputArr[]
for (int i = 1; i < 10; i++) {
digitsCount[i] += digitsCount[i - 1];
}
// Build the output array
for (int i = length - 1; i >= 0; i--) {
final item = array[i];
final digit = item ~/ exp % 10;
outputArr[digitsCount[digit] - 1] = item;
digitsCount[digit]--;
}
return outputArr;
}
/// The main function to that sorts a `List<int>` [array] using Radix sort
List<int> radixSort(List<int> array) {
// Find the maximum number to know number of digits
final maxNumber = getMax(array);
// Shallow copy of the input array
final sortedArr = List.of(array);
// Do counting sort for every digit. Note that instead of passing digit
// number, exp is passed. exp is 10^i, where i is current digit number
for (int exp = 1; maxNumber ~/ exp > 0; exp *= 10) {
final sortedIteration = countSort(sortedArr, exp);
sortedArr.clear();
sortedArr.addAll(sortedIteration);
}
return sortedArr;
}
void main() {
const array = [170, 45, 75, 90, 802, 24, 2, 66];
final sortedArray = radixSort(array);
print(sortedArray);
}
// This code is contributed by beeduhboodee
Output2 24 45 66 75 90 170 802
Time Complexity:
- Radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping the keys by the individual digits which share the same significant position and value. It has a time complexity of O(d * (n + b)), where d is the number of digits, n is the number of elements, and b is the base of the number system being used.
- In practical implementations, radix sort is often faster than other comparison-based sorting algorithms, such as quicksort or merge sort, for large datasets, especially when the keys have many digits. However, its time complexity grows linearly with the number of digits, and so it is not as efficient for small datasets.
Auxiliary Space:
- Radix sort also has a space complexity of O(n + b), where n is the number of elements and b is the base of the number system. This space complexity comes from the need to create buckets for each digit value and to copy the elements back to the original array after each digit has been sorted.
Frequently Asked Questions about RadixSort
Q1. Is Radix Sort preferable to Comparison based sorting algorithms like Quick-Sort?
If we have log2n bits for every digit, the running time of Radix appears to be better than Quick Sort for a wide range of input numbers. The constant factors hidden in asymptotic notation are higher for Radix Sort and Quick-Sort uses hardware caches more effectively. Also, Radix sort uses counting sort as a subroutine and counting sort takes extra space to sort numbers.
Q2. What if the elements are in the range from 1 to n2?
- The lower bound for the Comparison based sorting algorithm (Merge Sort, Heap Sort, Quick-Sort .. etc) is Ω(nLogn), i.e., they cannot do better than nLogn. Counting sort is a linear time sorting algorithm that sort in O(n+k) time when elements are in the range from 1 to k.
- We can’t use counting sort because counting sort will take O(n2) which is worse than comparison-based sorting algorithms. Can we sort such an array in linear time?
- Radix Sort is the answer. The idea of Radix Sort is to do digit-by-digit sorting starting from the least significant digit to the most significant digit. Radix sort uses counting sort as a subroutine to sort.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...