Puzzle | That’s impossible
Last Updated :
18 Sep, 2023
Puzzle 1: Rahul’s code did not pass all the test cases. As a result he’s been sentenced to Geeksville prison. The Geeks community is considerate towards its prisoners and sets them free if they solve a particular riddle. Geeks guard asks the following question to Rahul:
If I add 7 to a number I get 46. However, if I subtract 7 I get 30. The Geeks guard says :
I Know that I am correct. Tell me how is it possible??
Help Rahul get out of the prison.
Hint: Think a bit about number systems
Solution:
Clearly, the above puzzle seems to mathematically impossible. We have a number x.
x + 7 = 46
x = 39
by this logic
However
x - 7 = 30
x = 37
This inconsistency suggests that something is wrong with the assumptions that we are making. To solve this problem we need to think beyond what basic assumptions we make. Once we realize that the numbers might not be expressed in decimal number system, the problem becomes easy to solve. The question mentions the number 7.
So what’s the minimum base you start with??
0, 1, 2, 3, 4, 5, 6, 7 –> Base 8
When we check the addition in base 8 we get our solution.
37 in base 8 is the number.
37 – 40 – 41 – 42 – 43 – 44 – 45 – 46
Puzzle 2: Giving Rahul a second chance, Geeksguard asks him to divide a scalene triangle given into six equal areas.
Solution:
This is an easy puzzle if you don’t venture into thinking about circumcircles, 3-d ways to partition the triangle.
The area of a triangle is given by :
Area = 1 / 2 * base * height
Also we know that triangles between same parallel lines have the same height.
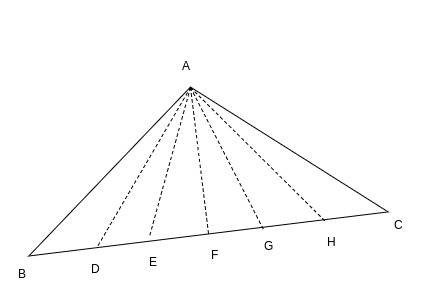
Here, we divide the base into six equal parts.
i.e. BD = DE = EF = FG = GH = HC
Height for all the sub triangles(i.e. AI) will stay the same.
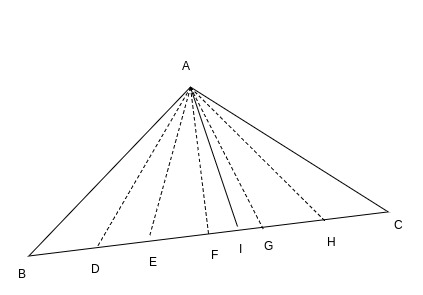
Hence, Area of triangles:
ABD, ADE, AEF, AFG, AGH, AHC is equal.
Another variation of this problem:
What if you were asked to solve the above problem, this time with a constraint:
You can only draw a maximum of three lines.
We use a property of triangles here. We know that a median divides a triangle into two equal areas.
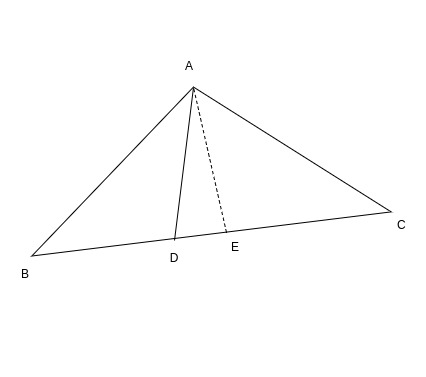
In the above figure, median AD divides the base into two equal halves. The height for both the triangles i.e. triangles ABD and ACD remains the same(i.e. AE). Also BD = DC
Area of triangle ABD = 1 / 2 * BD * AE = 1 / 2 * DC * AE = Area of triangle ADC
Therefore, area of both triangles becomes the same.
Let us assume that area of triangle ABC is 2a then we can easily see that area of triangles ABD and ADC become a each.
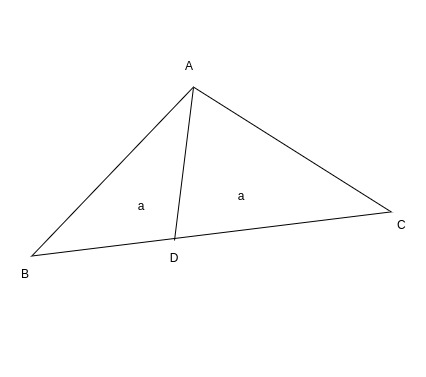
So drawing three medians would create six equal areas. To understand this in a better way, let us assume that the area of our triangle is 2a. Now when we draw a median it divides the triangle into two equal areas( i.e. a and a)
When three medians are drawn we can easily say that:
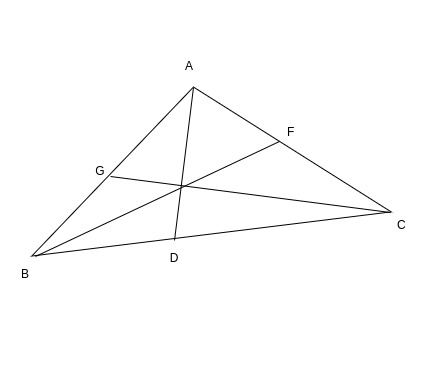
Here we have the three medians BF, CG and AD.
Median AD divides the triangle into two equal areas: ABD and ACD
Median BF divides the triangle into two equal areas: ABF and BCF
Median CG divides the triangle into two equal areas: ACG and BCG
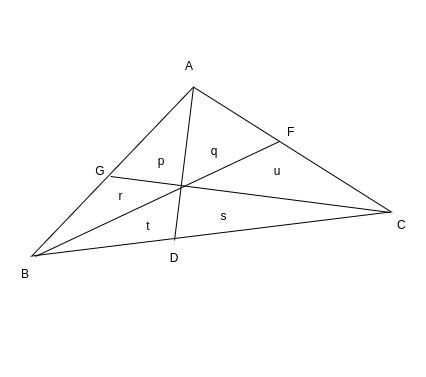
If the triangle of total area equal to 2a was divided by respective triangles into areas p, q, r, s, t, u then we would have:
p + r + t = q + u + s = a
r + p + q = t + s + u = a
p + q + u = r + t + s = a
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...