Puzzle 14 | (Strategy for a 2 Player Coin Game)
Last Updated :
19 Jan, 2023
Puzzle: Consider a two-player coin game where each Player A and Player B gets the turn one by one. There is a row of even number of coins, and a player on his/her turn can pick a coin from any of the two corners of the row. The player that collects coins with more value wins the game. Develop a strategy for the player making the first turn i.e, Player A, such that he/she never loses the game. Note that the strategy to pick a maximum of two corners may not work. In the following example, the first player, Player A loses the game when he/she uses a strategy to pick a maximum of two corners.
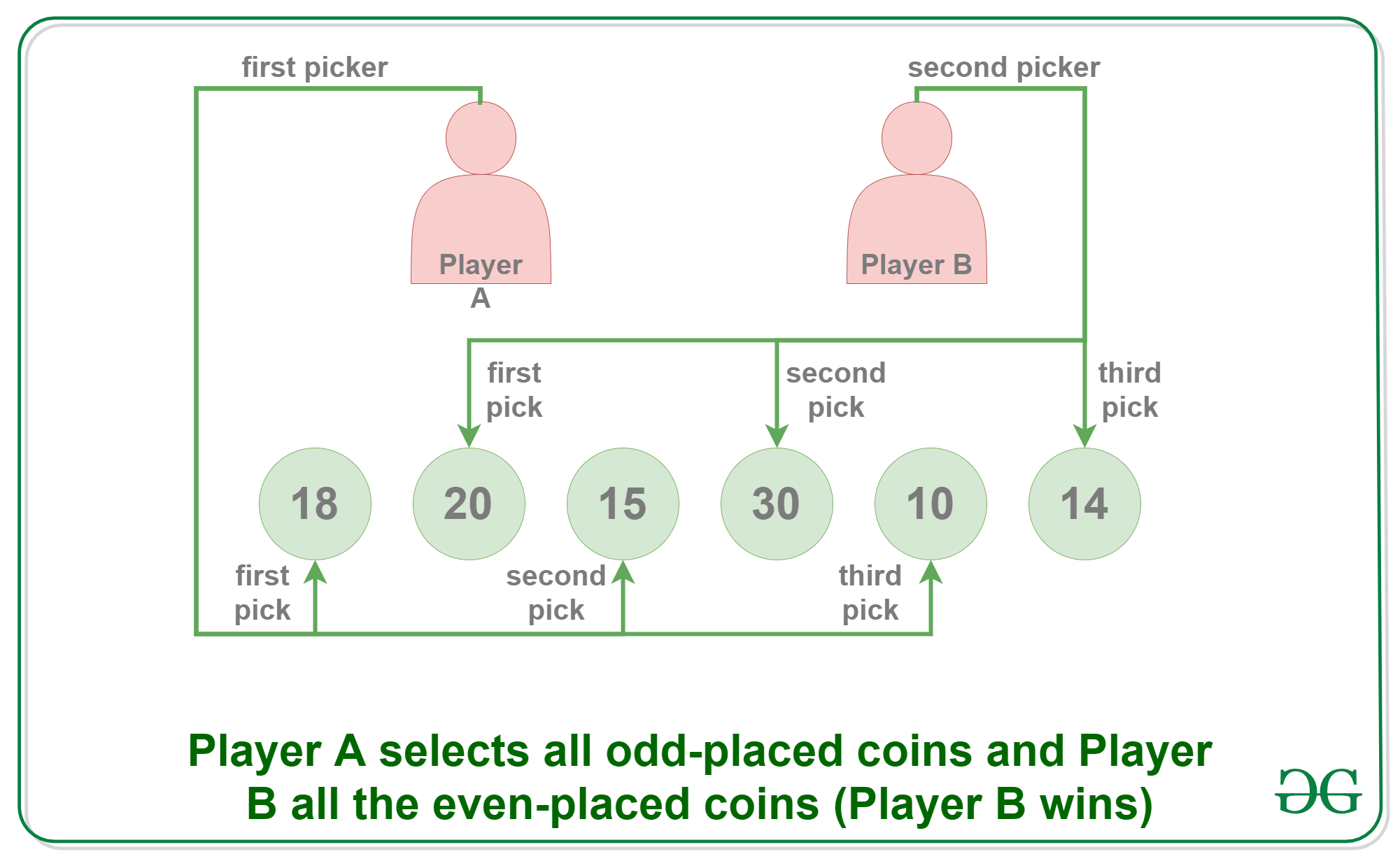
Example:
Initial row: 18 20 15 30 10 14
Player A picks 18, now row of coins is
After first pick: 20 15 30 10 14
Player B picks 20, now row of coins is
After second pick: 15 30 10 14
Player A picks 15, now row of coins is
After third pick: 30 10 14
Player B picks 30, now row of coins is
After 4th pick: 10 14
Player A picks 14, now row of coins is
Last pick: 10
Player B picks 10, game over.
The total value collected by Player B is more (20 +
30 + 10) compared to first player (18 + 15 + 14).
So the second picker, Player B wins.
Solution: The idea is to count the sum of values of all even coins and odd coins, compare the two values. The player that makes the first move can always make sure that the other player is never able to choose an even coin if the sum of even coins is higher. Similarly, he/she can make sure that the other player is never able to choose an odd coin if the sum of odd coins is higher. So here are the steps to a proper algorithm of either winning the game or getting a tie:
- Step 1: Count the sum of all the coins in the even places(2nd, 4th, 6th and so on). Let the sum be “EVEN”.
- Step 2: Count the sum of all the coins in the odd places(1st, 3rd, 5th and so on). Let the sum be “ODD”.
- Step 3: Compare the value of EVEN and ODD and this is how the first player, here Player A must begin its selection.
- if (EVEN > ODD), start choosing from the right-hand corner and select all the even placed coins.
- if (EVEN < ODD), start choosing from the left-hand corner and select all the odd placed coins.
- if (EVEN == ODD), choosing only the odd-placed or only the even placed coins will throw a tie.
Example: Suppose you are given the following rows of coins:
18 20 15 30 10 14
Coins at even places: 20, 30, 14 Coins at odd places: 18, 15, 10 These places are fixed independent of whether the choice of selection must begin from the left or the right-hand side.
Step 1: Sum of all even placed coins = 20 + 30 + 14 = 64
Step 2: Sum of all odd placed coins = 18 + 15 + 10 = 43
Step 3: Comparing the even and the odd placed coins where EVEN > ODD Therefore, Player A must start selecting from the right-hand side and choose all the even-placed coins every time(here they are 14, 30 and 20). So first picker, Player A picks 14. Now, irrespective of whether the second Player B starts selecting from the left-hand side i.e., 18 or from the right-hand side i.e., 10, the even placed coins i.e., 14, 30 and 20 are booked for the Player A. Therefore, be it any situation that arises, the first picker Player A will always win the game.
Illustration: Here are the illustrations to both the cases of pick by Player B:
Case 1: When Player B starts picking from the left corner.  Case 2: When Player B starts picking from the right corner after Player A.
Case 2: When Player B starts picking from the right corner after Player A. 
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...